54

Chika Ofili, a 12-year-old Nigerian boy based in the United Kingdom, has received the ‘TruLittle Hero Awards’ for discovering a new mathematical formula. Source

According to the above website (and several others), he envisioned a simple method to determine if a number is divisible by 7 (which was not included in his textbook), which is amazing on its own!

However, I am bothered by the claim of this being a new mathematical formula.

Is this really new?

Pedro A
  • 640
  • 1
  • 5
  • 10
  • 6
    What does it mean to be "based in the United Kingdom", anyway? To live somewhere without being a citizen? – Dmitry Grigoryev Nov 21 '19 at 12:54
  • 2
    @DmitryGrigoryev This is a quote from nigerianeye.com. I guess, that they want to emphasize that the boy doesn't live in Nigeria right now. I wouldn't read too much into that. – default locale Nov 21 '19 at 13:02
  • 5
    @defaultlocale I also assumed that "based in the United Kingdom" implies he doesn't live in Nigeria. I'm trying to understand why they couldn't just say "a boy from UK". – Dmitry Grigoryev Nov 21 '19 at 13:15
  • 29
    @DmitryGrigoryev , it's simply a newspaper *in Nigeria*. The boy is Nigerian, he is a Nigerian citizen, he was born in Nigeria ... he happens to be living in the UK. Not a big deal. – Fattie Nov 21 '19 at 14:21
  • I was reading "SHORT-CUT MATH" by Gerard W. Kelly (Published by Dover Books). On page 75 it says "There is no simple test for divisibility by 7". It turns out "Chika's Divisibility by 7 Test" is very simple and straightforward. Whether this mathematical formula is **new** is **not important**. What is clear is that it is not generally known. Many mathematical properties and algorithms are discovered and then independently **rediscovered** - Pythagoras, Levenburg-Marquardt, and so many others. "Chika's Test" makes us wonder if there is a universal generalization, which would be profound. – Xofo Feb 16 '22 at 18:00

4 Answers4

90

The Math.SE question about the method (Why does Chika Ofili's method for checking divisibility for 7 work?) is closed as a duplicate of an earlier, more generic, question (Divisibility criteria for 7,11,13,17,19) about divisibility tests for various prime numbers. The answer by @VitthalJadhav, posted back in 2013 includes Chica Ofili's formula verbatim:

(VJ's universal divisibility test)
7|10T+U if and only if 7|(1T−2U), or
7|10T+U if and only if 7|(2T+3U), or
7|10T+U if and only if 7|(T+5U) etc.

The last line means that the number 10T+U is divisible by 7 if and only if the number T+5U is divisible by 7.

The same technique is mentioned in the article "Puzzles, Pastimes, Problems" (Mathematics in School, Vol. 16, No. 5, November 1987), by D. B. Eperson (kudos to @DavePHD for finding this link):

My alternative test for multiples of 7 is, multiply the units digit by 5, and add this to the number formed by the other digits, and if the sum is a multiple of 7, then the tested number is also the multiple of 7.

So, evidently, this is not a new mathematical formula.

Is this method memorable and easy to use? Yes

Is it cool that 12 year old derived it on his own? Yes, kind of.

Is this a new mathematical formula, discovered in 2019? No, it was posted verbatim on Stack Exchange in 2013.

Is this a new mathematical formula, discovered in 2013? No, another answer by @labbhattacharjee shows the method to derive a formula like this for any number using the basics of number theory, established in XVIII century (works of Bézout, Gauss and many others).

Another, but very similar, method to test for divisibility by 7, is posted all over the internet (1, 2, 3) and was published at least as early as 1889 (Nature volume 40, Some Properties of the Number 7, R. TUCKER):

My attention was recently drawn by a pupil to the following property, which will be best illustrated by working out a particular example:

Let N  = 3425443
    u2 =  342538 i.e. u2 = 342544 - 2x3
    u3 =   34237 i.e. u3 =  34253 - 2x8
    u4 =    3409 i.e. u4 =   3423 - 2x7
    u5 =     322 and so on:
              28

if any of the quantities u2, u3, u4, &c., is divisible by 7, then N is so divisible.

Unlike Ofili's teacher, R. Tucker of University College School provides proof for this test and uses it as a part of a broader theorem. Also unlike Ofili's teacher, R. Tucker doesn't give any credit to his pupil.

This is, essentially, a formula that reduces 10T+U to T-2U. With one trivial step, we can go from T-2U to T-2U+7U = T+5U.

As a matter of fact, Ofili's teacher acknowledges that "minus 2" method is well known and she found references to it while researching the problem (Chika's Test):

... And furthermore, it works if you double the last digit and then subtract it from the remaining part of the number, of if you multiply the last digit by 9, 16, 23, 30 … and subtract. And actually the doubling and subtracting test can be easily found on the internet.

But we both agreed multiplying the last digit by 5 and adding it to the remaining part of the number is much more appealing! ...

L. E. Dickson's History of the Theory of Numbers attributes this particular divisibility test to A. Zbikowski (Note sur la divisibilite des nombres (Bull. Acad. Imp. Sci. Saint-Petersbourg 3 (1861)). Zbikowski mentions T-2U manoeuvre as a special case of a broader approach to create divisibility tests for an arbitrary divisor.

P.S. This reminds me a famous anecdote about Gauss deriving a formula for arithmetic series when he was 7. It wasn't a new formula even in 1780s, but still it was kinda cool that a primary schooler derived it on his own.

Community
  • 1
default locale
  • 2,079
  • 3
  • 24
  • 26
  • 3
    I recalled seeing something like this method in a Murderous Maths book back in the early 2000s, and this specific one is also found on their gloriously of-the-time website here at least as far back as 2001 on wayback: https://web.archive.org/web/20010308060326/http://www.murderousmaths.co.uk/books/BKMM1x11.htm – CriminallyVulgar Nov 21 '19 at 11:52
  • 5
    @CriminallyVulgar Thank you for the link. I'm pretty confident that both methods ("-2" and "+5") are much older than that. "-2" method was published in "Theory of arithmetic" in 1967 ([link](https://books.google.com/books?id=STpPAQAAIAAJ&q=%22divisible+by+7%22)). I didn't pinpoint the date of first publication, but I think 19th century would be a reasonable guess. In fact, I wouldn't be terribly surprised to find a method like this in the works of [al-Khwarizmi](https://en.wikipedia.org/wiki/Muhammad_ibn_Musa_al-Khwarizmi) (9th century). – default locale Nov 21 '19 at 12:13
  • 15
    Or that the 12 year old kid have internet acces and SE is googlable. – SZCZERZO KŁY Nov 21 '19 at 12:53
  • 31
    This reminds me of news about a Russian undergrad writing [his own OS](https://sourceforge.net/projects/bolgenos/) which later turned out to be a repackaged clone of Ubuntu. Media will sure go to great lengths to make a story news-worthy. – Dmitry Grigoryev Nov 21 '19 at 13:16
  • 1
    @defaultlocale It *does* depend on using place notation. al-Khwarizmi used place notation, but this wouldn't work in Roman notation (unless you use M->C->X->I + D->L->V) – Martin Bonner supports Monica Nov 21 '19 at 15:24
  • 2
    @CriminallyVulgar it is in the November 1987 "Puzzles, Pastimes, Problems", by D. B. Eperson, in the journal *Mathematics in School*, Vol. 16, No. 5, pp. 18-19, 34-35, which says: "My alternative test for multiples of 7 is, multiply the units digit by 5, and add this to the number formed by the other digits, and if the sum is a multiple of 7, then the..." https://www.jstor.org/stable/30214392?seq=1#page_scan_tab_contents – DavePhD Nov 21 '19 at 19:56
  • @MartinBonnersupportsMonica Surely, the test is more convenient with place notation, but, technically, it doesn't depend on notation at all and can be explained in terms of tens and ones, without writing numbers down (see [a similar test](https://www.sefaria.org/Avodah_Zarah.9b.2?ven=Sefaria_Community_Translation&lang=bi) in Talmud). Anyway, L.E. Dickson writes that al-Khwarizmi didn't provide the test for 7. Others, like Ibn al-Banna', Paciuolo, Rav Huna came up with different, more complicated tests. – default locale Nov 21 '19 at 20:00
  • 1
    @DavePhD Great Find! Thank you very much! – default locale Nov 21 '19 at 20:16
  • @Mar The test really works on polynomials, not radix notation, i.e. the digits can be arbitrary integers. If p(x) is a polynomial with integer coef's then 7 | p(10) <=> 7 | p'(10)+5p(0) <=> 7 | p''(10) + 5 p'(0) + 5^2 p(0) ... where p'(x) = (p(x)-p(0))/x. Here we can replace 5^2 by 4, being congruent mod 7. Iterated fully this yields the test of Crelle cited in my answer, a multi-digit extension of the OP test, i.e. it splits off many (vs. one) digit/coef at a time. – Bill Dubuque Nov 22 '19 at 00:31
  • 2
    Well, in 5th grade, I had "discovered" on my own that if the digits of a number were added up and it summed to 9, the original number is divisible by 9. Later I found out this was a well known math concept. If it weren't for our ancestors, many of us could've achieved unparalled greatness! ;-) Tomorrow I'm going to discover a recipe for French toast! – Nav Nov 22 '19 at 14:01
  • 2
    @Nav I say, they need to create 'TruBiggHero Award' for adults that make important everyday discoveries on their own. All those Nobel prizes and PHDs are practically unachievable for us regular folks and that's unfair – default locale Nov 22 '19 at 14:31
  • Maybe I'm not understanding what how the "|" symbol is being used (I'm familiar with this as a bit-wise or, which doesn't make sense here), but I don't really see how this formula is very useful since it seems you have to determine the divisibility of another similar in length number by 7. I might as well say, "I can check if any number is divisible by 7 by doing long division and seeing if there is a remainder". – Michael Nov 23 '19 at 03:28
  • 1
    @Michael It's just standard mathematical notation: if a,b are integers, we write "a|b" (read: 'a divides b') if there is another integer c such that b=ac. I'm pretty sure this predates the usage of | as a bitwise operator by a fair amount of time. – Denis Nardin Nov 23 '19 at 12:52
  • @DmitryGrigoryev Even if an undergrad _did_ write their own OS from scratch, it wouldn't be particularly newsworthy. Literally every CS undergrad did this at the university I graduated from and I suspect that isn't particularly unusual. It was a fun project, but hardly newsworthy. – reirab Nov 24 '19 at 08:08
  • Is it cool that 12 year old derived it on his own? **Yes.** Many mathematical formulas that have been discovered often are co-named with the originator and the person who rediscovered it. I would say that it is quite awesome a 12-year-old rediscovered this property. – Xofo Feb 16 '22 at 18:08
19

This and related divisibility tests are ancient and well-known to most who have mastered a first course in elementary number theory. They go back at least a couple hundred years, and possibly even much further (e.g. possibly to circa 1200 given Leonardo Pisano (b.k.a. Fibonacci) discussed tests for divisibility by 7,9,11 in his Liber Abaci (Book of Calculation))

For example, Dickson's History, v.1 p. 339 cites a general divisibility test credited to A. L. Crelle in 1844 which has the above test as a special case. I quote Dickson in the 4 bold lines below:

enter image description here enter image description here enter image description here

The prior 3 paragraphs are excerpted from one of my math.SE posts, which has further remarks.

Questions about such divisibility tests are FAQs in general-level math forums like math.SE and sci.math. There are thousands of posts discussing such in their archives, including many that explain (in modern language) the above general idea used by Crelle, e.g. here on math.SE. Almost everyone who has mastered a course in elementary number theory knows these ideas well (or could easily derive them if need be).

However, except for a few common cases (e.g. casting out nines and elevens) such divisibility tests generally are not named, nor are they attributed to anyone (which is typical for very old elementary results that are easier to (re)derive than to locate citations for - even more so for results like this that are less useful nowadays given the ubiquity of calculators and computers)

Bill Dubuque
  • 465
  • 3
  • 9
  • Can you clarify whether the second image is your own work, or if it is a quote of a reference? – DavePhD Nov 21 '19 at 21:48
  • 1
    Only the first image (the 4 boldest lines of text) is quoted (excerpted from the linked page of Dickson's History). The latter images are my explanation of how that method of Crelle specializes to this particular test (for A = 10, s = 7, m = 1 = r, n = 5) , etc. – Bill Dubuque Nov 22 '19 at 13:59
  • This is Crelle's 1844 article: https://www.digizeitschriften.de/download/PPN243919689_0027/PPN243919689_0027___log15.pdf – DavePhD Nov 24 '19 at 20:57
  • 1
    @DavePhD Yes, I was perusing that a few days ago and plan to update the answer with that and more when time frees up. Till then I will merely add the he does *explicitly* mention the inverse choice n = 5 (vs. -2) for 1/10 (mod 7) on p.130 #23 – Bill Dubuque Nov 24 '19 at 21:30
4

If 12 - 13 year primary school student doesn't know algebra & it recognise pattern in math - develop divisibility test then yes it is invention for him. Is it new discovery in math ? No. Test given by Chika is too old. It is also in BKT's 'Vedic Mathematics' book - Published in 1965. I had given general Theorem (called Cross Divisibility Theorem) to derive divisibility test for any natural number in book
"Modern Approach to Speed Math Secret" published in 2013.

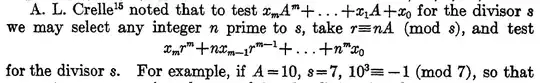
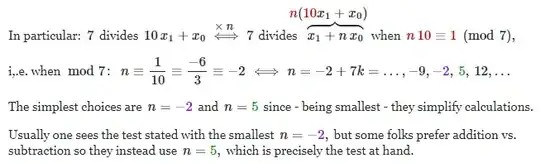
enter image description here enter image description here For Video explanation refer https://youtu.be/RB9xU0b5AW4

Vitthal Jadhav
  • 49
  • 2
  • 2
    So you're the Vitthal Jadhav mentioned in [this answer](https://skeptics.stackexchange.com/a/45432/39658)? Well, you can't get much more authoritative than that, then. Welcome to Skeptics.SE! – F1Krazy Nov 22 '19 at 21:34
  • link to page of the 1965 book: https://archive.org/details/VedicMathematicsJagatguruSankracharaya/page/n331 – DavePhD Nov 23 '19 at 02:04
  • 2
    **Your general test is exactly the same as the 1844 Crelle test I cited.** It's trivial using modern algebra and *modular* fractions: mod aB-b: B = b/a so 0 = G(B) = G(b/a) <=> 0 = a^m G(b/a) = G_m b^m + ... + G_0 a^m. So it boils down to scaling by a^m to clear the denominators - just as with *rational fractions*.Here G(x) = sum_k G_k x^k is the associated polynomial. Note a is invertible mod aB-b by (a,aB-b) = (a,b) = 1 by Euclid. – Bill Dubuque Nov 23 '19 at 03:26
  • 1
    Friends , I discovered this Theorem independently. I never read such Theorem like crelles test before it. No problem, I will make changes in next edition of "Modern Approach to Speed Math (https://play.google.com/store/books/details/Vitthal_B_Jadhav_Modern_Approach_to_Speed_Math_Sec?id=XH51DwAAQBAJ) " . F1Crazy I independently invented many algorithm , methods - Also raised voice against 'Vedic Mathematics' for calling it Vedic by neglecting other indian mathematicians contribution by BKT. I won't mind to give credit to crelle. In next edition I will rename the test & give credit to Crelle. – Vitthal Jadhav Nov 24 '19 at 09:15
  • 2
    Man's existence doesn't lies in name. I invented more advanced Theorem than this. Frankly speaking - In universe no one invent 100 % by their own. We stand on each others shoulder. You can omit my name from this test & just call cross Divisibility test or Crelles Theorem / test. Crelle is getting credits & his work will known to many due to this post & my rediscovery of Theorem. I am happy for that. – Vitthal Jadhav Nov 24 '19 at 09:19
2

This was published in 1965 as rule no 2 for divisibility by 7 in Vedic Maths. Here’s a blog post from 2009 about it http://blogannath.blogspot.com/2009/10/vedic-mathematics-lesson-23.html?m=1

Edit: here’s a Wikipedia link showing Vedic Maths was published in 1965. https://en.m.wikipedia.org/wiki/Vedic_Maths

Paul McFarling
  • 37
  • 3
  • 1
    Nice find, +1 :) I wonder, is it possible to trace this technique back to Vedas? – default locale Nov 21 '19 at 16:50
  • 4
    The link in the answer doesn't say anything about "1965". – DavePhD Nov 21 '19 at 19:48
  • 2
    @defaultlocale After a brief search, the precise formula doesn't exist, but given that the idea of units and irreducibles in modulo rings were discussed in brief in the Vedas, I think that's close enough to saying that this technique is in there. – Rushabh Mehta Nov 21 '19 at 23:51
  • 2
    The claim in the blog is hearsay without any specific citation to the test in said 1965 book. Further, one should be skeptical of any historical claims in "Vedicts Maths" given that the linked Wikipedia article cites reputable scholars who are highly critical of its historical accuracy ("adhering to dubious historiographical standards"). But it is a moot point since we already know much earlier uses, e.g. in 1844 by Crelle (see my answer). @Don I don't agree that discussion of modular units (again citation needed) necessarily implies knowledge of this test. – Bill Dubuque Nov 22 '19 at 15:35
  • 2
    **Beware** that there is an error in the linked blog post: it implies that the first presented divisibility by 7 test (10T+U -> T - 2U) can be used to compute the remainder, which is false, since, mod 7, the test amounts to multiplying by -2 which generally *changes* the remainder (when nonzero). None of the rules that split off *least* significant digits this way will preserve the remainder. For that we need to work from the other end with the *most* signfificant digits, e.g. see the [*unversal* divisibility test](https://math.stackexchange.com/a/2063944/242) linked in my answer here. – Bill Dubuque Nov 22 '19 at 16:04
  • Clearly the test given in Vedict Maths is exactly the same test in question. Therefore, the kid wasn’t the first to come up with it. I was making no claim beyond that. I don’t believe the credibility or accuracy of the source matters much in this instance other than to say the exact same thing existed prior to Chika “discovering” it. – Paul McFarling Nov 22 '19 at 18:12
  • @BillDubuque Here is a link to the correct page of the actual book https://archive.org/details/VedicMathematicsJagatguruSankracharaya/page/n331 (page 274 according to the book's numbering) – DavePhD Nov 23 '19 at 02:09