Prabowo Subianto, a leading opposition leader in Indonesia, claims that Indonesian's Gini coefficient is 49%, and that that means 1% of Indonesian own 49% of the wealth.
The text said that Gini ratio in Indonesia according to Credit Suisse is 0.49. That means 1% richest control 49% wealth.
As you have surmised, this is not the correct way to understand a Gini coefficient. Wikipedia explains:
There are some issues in interpreting a Gini coefficient. The same value may result from many different distribution curves.
There are several sources of estimates for Indonesia's Gini coefficient(s).
The original claim appears to refer to the 2016 Global Wealth Data Book.
In table 3-1, on page 107, it lists Indonesia as having a Gini % (referring to wealth) as 84% - worse (subjectively) than the claim.
In table 1-5. on page 16, it shows that, in 2014, the top 10% of the population owned 36.4% of the wealth - better (subjectively) than the claim.
The same report was updated a year later: 2017 Global Wealth Data Book.
The updated figures have Indonesia at 83.7% Gini coefficient (for wealth).
The new report also includes older figures for Indonesia - back in 1997, the top 10% owned 65.4% of the wealth (far less evenly distributed than the 2014 estimates). But the 1997 figures also include the 1% numbers, so it goes straight to the heart of the claim: The top 1% owned 28.7% of the wealth in 1997 - and if the estimates are consistent, can be assume to own less now.
The Gini index for income has been estimated as 39.5 in 2013. (Sourced from the World Bank.)
In summary:
Quick answer... this guy is playing demagogue. He's pretending that the gini coefficient means things that it does not.... or perhaps he doesn't necessarily understand (or care) himself.
On the gini coefficient, I've found a blog by a math teacher that appears to lay it out pretty clearly.
[...]
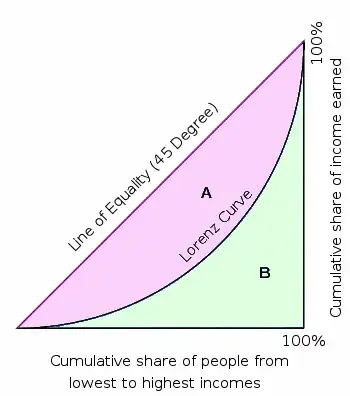
In plain English, the graph above indicates the proportion of the income going to the poorest people, middle-income people and richest people.
There will always be rich and poor, but we are interested in how evenly wealth is distributed and most governments put effort into keeping this coefficient as low as possible.
The Gini Coefficient ranges between 0 and 1 (or it can also be expressed as a number from 0 to 100) and is given by the ratio of the areas:
Gini Coefficient = {A}/{A+B}
If A = 0, it means the Lorenz Curve is actually the Line of Equality. In this case, the Gini Coefficient is 0 and it means there is "perfect" distribution of income (everyone earns the same amount).
If A is a very large area (making B very small), then the Gini Coefficient is large (almost 1) and it means there is very uneven distribution of income. Countries with a high Gini Coefficient are more likely to become unstable, since there is a large mass of poor people who are jealous of the small number of rich people.
It also seems to agree with what wikipedia has to say on the subject.
So... conclusion from that, it's possible to have a gini coefficient of .49 while 49% of the money is held by 1% of the people, but if I'm understanding the math correctly, it would mean that the money in the rest of the populace would be almost perfectly distributed. That's.. unlikely. Gini 0.49 is actually pretty good.
That's not what's going on, though. Credit Suisse databook 2016 (page 107) lists Indonesia as having a wealth gini of 84.0%, which is quite a lot worse than 49%. Based on that, it's possible that 1% of the population does hold 49% of the money, but it certainly doesn't follow directly.
now, the numbers do look fairly dire. It's not like his overall position about wealth distribution is unfounded... it's just that those numbers don't mean what he's saying they mean.
