Did Robert Hooke publish his spring force law as an anagram?

Question

Did Robert Hooke (and other contemporary scientists) ever publish their discoveries as anagrams?

This Wikipedia article claims that Robert Hooke published his spring force law as a anagram. It also goes on to say that,

This was a method sometimes used by scientists, such as Hooke, Huygens, Galileo, and others, to establish priority for a discovery without revealing details.

This page is what I could find on the net related to the Hooke claim. It says

When Robert Hooke discovered his law of elasticity in 1676, he didn’t publish it in the ordinary way. Instead, he published it as an anagram: “ceiiinosssttuv.” He revealed this two years later as the Latin ut tensio, sic vis, meaning “as the extension, so the force.” This ensured that if someone else made the same discovery, Hooke could reveal the anagram and claim priority, thus buying time in which he alone could build upon the discovery.

Many great scientists of the age, including Leonardo, Galileo and Huygens, used anagrams or ciphers for similar purposes. The Newton-Leibniz controversy over who invented calculus occurred because Newton claimed to have invented calculus in the 1660s and 1670s, but didn’t publish until 1693. In the meantime, Leibniz developed and published his own version of calculus.

How much of this is really true?

Answer 1

All of this is (mostly) true.

Ciphers and anagrams in 17th century scientific writing

Using anagrams and ciphers was a frequently used way to safeguard inventions and discoveries against intellectual theft in the seventeenth and eighteenth century. An early example can be found in a letter dated December 11, 1610 from Galileo Galilei to Johannes Kepler. The letter contains the Latin passage (translations are given in the referenced source):

Haec immatura a me iam frustra leguntur o y ("These, premature from me, are at present deceptively gathered together"),

which is an anagram of the sentence

Cynthiae figuras aemulatur mater amorum ("The mother of love [i.e. Venus] imitates the shapes of Cynthia [i.e. the moon]").

Apparently, Galileo is talking here in encrypted form about the different phases of the planet Venus, which resemble the phases of the moon.

The use of ciphers became a fairly standard way of documenting discoveries before their actual publication. This is illustrated for instance in the proceedings of the Royal Society meeting from February 4, 1668. Here, a letter by Christiaan Huygens is discussed in which Huygens explicitly proposes

a way of securing his discoveries and inventions for the future by way of cypher or anagram, to be lodged in the Register-book of the society, till he should think it convenient to explain them in a common language; making withal a beginning of this way of communicating new discoveries by sending the following cypher; which was ordered to be entered into the Register-book.

This is the cipher:

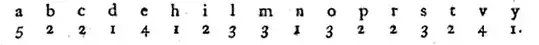
The same cipher occurs in one of Huygens' later writings together with the Latin sentence

Lens e duobus composita hyperbolicam aemulator ("a lens composed of two rivals the hyperbola")

The basic idea is that the number below each letter corresponds to the number of occurrences of that letter in the encrypted sentence, even though it doesn't quite work for this cipher: for example, the letter a occurs four, not five times in the decoded sentence.

The same passage in the proceedings of the Royal Society also presents a cipher by Christopher Wren, which he devised as a response to Huygens' cipher. Another famous example of the use of a cipher in seventeenth century scientific writing can be found in Isaak Newton's second letter to Leibniz from November 3, 1676. The paragraph explicitly states that it will use cipher to "register" Newton's findings, given as a fairly long number-letter combination (that I hopefully copied without a mistake from the article which discusses the letter):

Nevertheless – lest I seem to have said too much – inverse problems of tangents are within our power, and others more difficult than those, and to solve them I have used a twofold method of which one part is nearer, the other more general. At present I have thought fit to register them both by transposed letters, lest, through others obtaining the same result, I should be compelled to change the plan in some respects. 5accdæ10effh11i4l3m9n6oqqr8s11t9v3x: 11ab3cdd10eæg10ill4m7n6o3p3q6r5s11t8vx, 3acæ4egh5i4l4m5n8oq4r3s6t4vaaddæeeeeeiijmmnnooprrrsssssttuu

According to the author of the article, this translates to

Una Methodus consistit in extractione fluentis quantitatis ex æquatione simul involvente fluxionem ejus: altera tantum in assumptione Seriei pro quantitate qualibet incognita, ex qua cætera commodè derivari possunt, & in collatione terminorum homologorum æquationis resultantis, ad eruendos terminos assumptæ seriei.

("One method consists in extracting a fluent quantity from an equation at the same time involving its fluxion; but another by assuming a series for any unknown quantity whatever, from which the rest could conveniently be derived, and in collecting homologous terms of the resulting equation in order to elicit the terms of the assumed series.")

Thus, it's well-documented that ciphers were used by Galileo, Huygens, Wren, and Newton as a proof of inventorship in the 17th century.

Robert Hooke and the cipher ceiiinosssttuv

Being a leading member of the Royal Society, it's not surprising to find that Hooke was not only very familiar with the practice, but also used it extensively himself. The anagram that you mention in your question comes from Hooke's Descriptions of Helioscopes, which he concludes on page 31 with an outlook of future publications:

To fill the vacancy of the ensuing page, I have here added a decimate of the centesme of the Inventions I intend to publish, though possibly not in the same order, but as I can get opportunity and leasure; most of which, I hope, will be useful to Mankind, as they are yet unknown and new. [emphasis in the original]

Some of the ten "Inventions" are marked as "Discovered", and several of the others use ciphers. The one that you mention in your question is number 3 in that list:

The true Theory of Elasticity or Springiness, and a particular Explication thereof in several Subjects in which it is to be found: And the way of computing the velocity of Bodies moved by them, ceiiinosssttuu [emphasis in the original]

Hooke provides the solution to his anagram when he eventually publishes his Lectures De Potentia Restitutiva, or of Spring explaining the Power of Springing Bodies:

About two years since I printed this Theory in an Anagram at the end of my Book of the Descriptions of Helioscopes, viz. c e i i n o s s s t t u u, id est, Ut tensio sic vis; That is, The Power of any Spring is in the same proportion with the Tension thereof [emphasis in the original]

Note that the original spelling is slightly different from the one given in the question: In both the Descriptions and in Potentia Restitutiva, the last two letters are without doubt two u letters, whereas the anagram quoted in the question ends in uv. The second u apparently refers to the first letter of vis (apparently, words that started with the /v/ sound were spelled during the Renaissance using the letter v, but if the sound occurred within the word, the letter u was used).

Conclusion

It is attested that Galileo, Huygens, Hooke, Newton and others used ciphers and anagrams to establish priority for a discovery without revealing details. In particular, Hooke used the anagram "ceiinosssttuu" to ascertain the gist of his theory on springs, and he did reveal the solution to this anagram himself in a later publication.