15

Rob Hummer gave a talk at Cine Gear Expo 2011 about how film and digital cameras catch light.

He makes a handful of extraordinary claims about digital sensors - including a claim that you get dead pixels on camera sensors by bringing them on aircraft due to gamma radiation and that there's a cover up by camera makers about it.

There's a little problem though with digital cameras, I promise you.

Anyone ever take their cameras on an airplane? Ok, every time you do that you kill photo sites on your camera, because when Canon, Nikon, Casio, Panasonic ship cameras in North America, they do it by boat, and that's because you need about - at altitudes of 20,000 feet and higher - you need about 125 feet of concrete to shield yourself from the gamma rays of higher altitude. They don't hurt us, but gamma rays induce voltages in sensors that fry our pixels.

He goes on to give an anecdote about a set of cameras for a film shoot that were damaged in a 12-hour flight.

At DALSA, when I said we should tell people about this, they said "Oh no, we don't want people to know about this, because there will be a big class action lawsuit [...]

He explains software on the camera hides the damage caused by dead pixels, and that film is immune to gamma rays.

Considering people have been carrying digital cameras on airplanes for at least the last 15 or so years - do gamma rays actually damage a modern, or less modern digital sensor. Is film immune to this effect?

Community
  • 1
Journeyman Geek
  • 269
  • 1
  • 9
  • 8
    Clearly Hummer is confusing [gamma rays](https://en.wikipedia.org/wiki/Gamma_ray) with [cosmic rays](https://en.wikipedia.org/wiki/Cosmic_ray), which are completely different things. Also, he seems to think that the higher the shielding needed to stop a ray, the higher the chance a ray will interact with a camera. The opposite is true since "shielding" and "scattering" are the same thing, at their heart. – Sklivvz Jan 05 '18 at 10:05
  • To get visible blurring on a [2003-era] CMOS sensor it takes [at least 1kGy of gamma rays](http://www.sciencedirect.com/science/article/pii/S0026271403001379). That's about 6 orders of magnitude more than in a single flight. I don't know what it would take to damage a single pixel though. – Fizz Jan 05 '18 at 10:19
  • @Sklivvz he might be - even then, a massive conspiracy to hide dead pixels due to specific events in software sounds like a bit of a stretch, gamma rays, cosmic rays or solar flares. – Journeyman Geek Jan 05 '18 at 11:48
  • 6
    It is also worth to note that it is very common to use the sea to transfer cargo around just because it is cheaper, not because there is some weird gamma effect thingie going on. And how the hell satelittes work, then? I doubt we put so much concrete in orbit to shield then, and last time I checked Hubble didn't use film. – T. Sar Jan 05 '18 at 17:13
  • 3
    @T.Sar Hubble get its camera replaced every so many years. [WFPC2](https://en.wikipedia.org/wiki/Wide_Field_and_Planetary_Camera_2), one of its main cameras, was replaced a few years back because it had a bunch of hot pixels. Satellites that can't be reasonably serviced have relatively short operational lifetimes. Correcting for a few bad pixels in software is no big deal, and always done as part of the image reduction process to get rid of data from bad pixels. – KAI Jan 05 '18 at 18:43
  • 3
    @JourneymanGeek I think you are misunderstanding the claims about software corrections to bad pixels. When they say "hide" bad pixels, they mean that they make them go away because that's what any reasonable person would want. It isn't some secret or conspiracy. Procedures for doing this go under names like "pixel mapping", and are [advertised features](http://www.olympusamerica.com/crm/oneoffpages/ask_oly/crm_e_ask_oly_03_09.asp) of cameras. – KAI Jan 05 '18 at 19:01
  • @kai thanks for the info, I wasn't aware of this. – T. Sar Jan 05 '18 at 20:16
  • @Fizz Note that if your camera takes 1kGy you're not going to be around to care about bad pixels. That's a drop-in-your-tracks level dose. – Loren Pechtel Jan 06 '18 at 03:14
  • @KAI he does make it sound like a *massive* problem - I can get one of two pixels in I donno, 8 million dying. He makes it sound like the cameras were rendered unusable by this. – Journeyman Geek Jan 06 '18 at 03:31
  • 8
    No, film is not immune to gamma rays. On the contrary: photographic film (or rather: plates) is [how gamma rays were first discovered](https://en.wikipedia.org/wiki/Paul_Ulrich_Villard)! The claims here are bullshit because they ignore the fact that we are **always** subjected to radiation, so called [**background radiation**](https://xkcd.com/radiation/). At cruising altitude in an airline, there is slightly more radiation, yes. But apart from a slightly higher intensity, there is nothing magical about that, and it does not warrant a huge cover-up due to billions of pixels dying. –  Jan 08 '18 at 12:05
  • 1
    @MichaelKarnerfors: [20 times](https://www.youtube.com/watch?v=XuQgVGDENbU) is a bit more than "slightly". I agree about the film though. – Fizz Jan 09 '18 at 08:37
  • 2
    @Fizz Intensity multiplied by Exposure Time equals Dose. You spend **much** more than 20 times as much time on the ground than in flight. Sure, 2000% sounds like "OMG! That is sooo much!!!". But the relatively short time that it is actually subjected to it means that the accumulated dose is still a whole lot less compared to what the camera is subjected to over just one month. Since cameras go for **years** without degrading noticeably from background radiation, I still call BS on the original claims here. Which of course makes the subsequent claim of a coverup land in Tinfoil Hat-country. –  Jan 09 '18 at 08:44
  • 1
    @MichaelKarnerfors: It depends [how often you fly](http://www.businessinsider.com/airplane-flight-cosmic-radiation-exposure-altitude-2015-11) "the National Council on Radiation Protection and Measurements reported in 2009 that aircrews have, on average, the highest yearly dose of radiation out of all radiation-exposed workers in the US." – Fizz Jan 09 '18 at 08:47
  • @MichaelKarnerfors: "The annual hit to aircrews is an estimated 3 millisieverts (mSv) — a complicated-sounding measure of the amount of background radiation a person receives in one year in the US — which beats out the annual doses received by other high-radiation jobs, such as X-ray technicians and nuclear power workers. (Only astronauts are more exposed; 10 days in spaces delivers about 4.3 mSv to the skin alone, which is about 4.3 years' worth of cosmic radiation on the surface of Earth.)" – Fizz Jan 09 '18 at 08:47
  • @Fizz Yes that is true but that exposure is still not significant. If the original claim was true we would see a whole lot more camera damage from cameras just being on the ground, or by living in a place like Denver. If the original claim was true, cameras in Dever would degrade significantly faster than cameras in the lowlands, but I have yet to hear anyone make any such claim. I am sorry but the whole original statement **reeks** of the common misconception that in normal daily life there is no radiation around us, which is nonsense. –  Jan 09 '18 at 08:52
  • 1
    [According to Don Pettit](http://www.tested.com/science/space/455640-how-cosmic-rays-damage-camera-sensors-space/) "After about a year [on the ISS], the images they [cameras] produce look like they are covered with electronic snow." So I'm guessing the new equipment is more sensitive than the 2003 era one. – Fizz Jan 09 '18 at 09:06
  • Let us [continue this discussion in chat](http://chat.stackexchange.com/rooms/71385/discussion-between-michael-karnerfors-and-fizz). –  Jan 09 '18 at 10:24
  • @T.Sar Satellites use space-hardened hardware that typically costs some 1000x more than the equivalent hardware for use on the ground, exactly because of shielding to the harsh space environment. – gerrit Jan 09 '18 at 11:47
  • Cosmic ray flux in the upper atmosphere is far more than 20x higher than on the surface. The surface sees mostly secondary particles at much lower energies. For example, see [this article](http://www.thespacereview.com/article/464/1). Airlines don't fly high enough for this to to be a problem, but it is a problem for suborbital (space)flights. – gerrit Jan 09 '18 at 11:53

2 Answers2

17

Robert Hummel's claims are quite inaccurate, in a number of ways.

The gamma ray flux on Earth

Earth's atmosphere is effectively opaque to gamma rays and cosmic rays, the latter of which are high-energy protons or the ionized nuclei of other elements. Gamma rays - in particular high energy gamma rays - are emitted by objects like active galaxies, pulsar wind nebulae, and gamma ray burst progenitors. They create a spectrum that can be roughly described as a two-part broken power law that decreases with increasing energy.

The vast majority of gamma rays that reach Earth collide with particles in Earth's atmosphere at altitudes of 20-30 km (see Ozlem Celik's PhD thesis), 3-5 times as high as the altitudes Hummer is referring to. They create electron-positron pairs, which then lose energy through a mechanism called bremsstrahlung, in turn emitting more photons, which create more electron-positron pairs. This is what we call an air shower, and even though (optical) radiation from these particles will eventually reach Earth's surface, large amounts of it will be dissipated (Abeysekara et al. 2017). Even the air shower from a 1 TeV gamma ray will lose ~93% of its energy by the time it hits the ground, and at 20,000 feet, the remaining energy should still be significantly small.

To quantify this a bit more, we can say that the atmosphere has a thickness of 1000 grams per square centimeter, or about 28 radiation lengths (Funk 2015; arXiv version). The radiation length is the distance over which the gamma ray flux decreases by a factor of 1/e; it is roughly 37.7 grams per square centimeter (see Celik). (Side note: Funk says that Earth's atmosphere is equivalent to about 1 meter of lead, which means that Hummer's claim of 125 meters of concrete shielding is a little unlikely, as the gamma ray flux through that much material would seem to be quite close to zero.)

We can convert an altitude to radiation lengths by linearly integrating the density of air to a given altitude. At 13,000 feet, the atmosphere has a depth of 16.7 radiation lengths; at 36,000 feet, this is 6.1 radiation lengths. At 20,000 feet, somewhere in the middle (~12) seems reasonable, meaning that a camera at 20,000 feet will receive e28-12 = e16 = 8.8 million times as much radiation (roughly) as a camera on the ground.

How much is needed to damage a camera?

Not surprisingly, scientists care about how much damage instruments suffer from radiation, including gamma rays and cosmic rays. It turns out that the performance of a high-resolution (AVT Marlin F-145C2) camera degrades at exposures of about 100 milliSieverts per hour of low-energy (100 keV - 1.5 MeV) gamma rays (Marbs & Boochs 2006).

Now, Earth does receive higher energy gamma rays - for instance, we see particularly interesting high-energy (TeV and, rarely, PeV) emission from various galactic and extragalactic sources. However, both the cosmic ray and gamma ray spectra follow a sharply decreasing double broken power law with increasing energy. Here, for instance, is the cosmic ray spectrum incident on Earth's atmosphere, from 1 GeV up (image credit: IceCube):

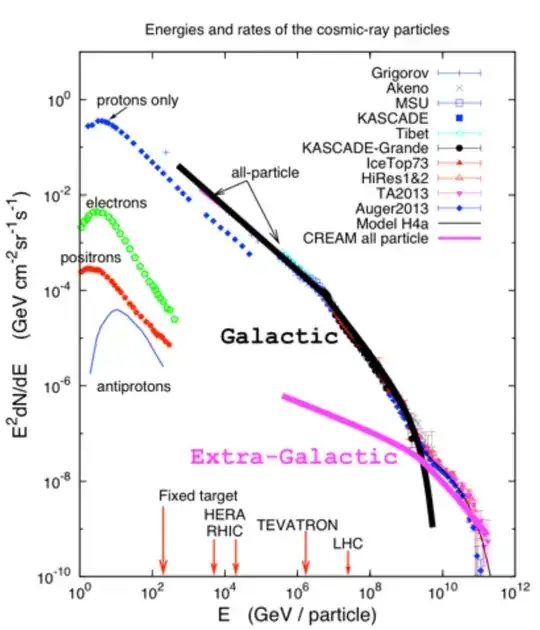
Cosmic ray spectrum

At 100 MeV, this may mean rates as high as 100 particles per square meter per second. However, after the attenuation of the Earth's atmosphere, this flux drops substantially, as we showed before. Go up by an order of magnitude in energy and your particle flux drops off by a factor of 100 or so, meaning the contribution of high-energy gamma rays is not substantial. I would argue that the analysis of the authors is applicable to the high-energy portion of the spectrum, too, simply because a camera at 20,000 feet will not be exposed to many high-energy particles on a flight of a few hours.

At even 10,000 feet, a human is exposed to about 5 microSieverts per hour; a camera would presumably be exposed to even less. Even 5 microSieverts per hour, however, is substantially smaller than the threshold given by Marbs & Boochs. Moreover, if I wanted to be nitpicky, this figure includes cosmic rays, not just gamma rays; the gamma ray contribution would be much smaller.

I think we can definitively say that no, gamma rays on an airplane will not damage a digital camera. In outer space, without the protection of Earth's atmosphere? Yes, both cameras and film can be quite easily damaged by cosmic rays and gamma rays.

For context, I'm currently doing work in ground-based gamma-ray astronomy as part of the VERITAS group.

Community
  • 1
HDE 226868
  • 11,143
  • 5
  • 61
  • 65
-1

This may have been some technical inaccuracies of Mr. Hummel's presentation but the intention and spirit behind it is accurate.

HDE 226868 makes some strong assumption as to both flight time and altitude, but did not take in the fact the particular thresholds that sensor manufacturers actually look at for significant damage, which still is likely not enough for the typical consumer to see. Also, the problem mostly comes with larger and more complex higher photosite count sensors, not the ones that most consumers have.

Hummell is also technically correct that it's a "cover-up," in so far that manufacturers do not tell customers of the real damage that accumulates particularly on long haul flights (over 6-hours at altitudes above 30,000'.)

There are plenty of damaging things you can do to any consumer product you own if you don't know where the harm originates. Plenty of people think that any food container is "microwave safe," and that is just not the case. You can test and observe damage accumulating over time. You don't see any camera manufacturer saying "airplane safe" or X-ray safe, because most people don't realize that there is any damage that being caused in the first place.

There's quite a bit of information that been published over the years about this and having worked for a sensor manufacturer can tell you that this is 100% true and well known in sensor manufacturing circles. It's not something that any of the manufacturing companies want to talk about, but its is extremely well known.

An aside, some sensors are manufactured specifically due to the susceptibility to different types of radiation. There are some DIY and lower end detectors/dosimeters made from repurposed imaging sensors, it's an interesting engineering pastime if someone was so inclined.

My first google search returned this whitepaper which explains the situation quite well even if it's not exactly apples to apples. High altitude, length of flight, size and complexity of imaging sensor are all factors for cosmic ray damage.

http://ridl.cfd.rit.edu/products/publications/May_2017_Moser_Final_Paper.pdf

Hope this helps add more clarity.

Joe

Joe2112
  • 11
  • 2
    Hi, Joe. I'd like to note that the pdf you link to is talking about cosmic rays - high-energy relativistic light nuclei - rather than gamma rays. – HDE 226868 Aug 22 '20 at 16:51