12

I remember vividly that when i still was young, I'd examine the snow as it dropped on my winter cloths. Every time I was amazed by the nice textures I discovered. Now many years later, I'm wondering if there's a possibility that crystals can be exactly the same.

From "Everyday Mysteries", I learned that there are a lot of snow crystals each winter (a trillion trillion). As you can imagine, going through all of them isn't really possible. Therefore, they suggest to rely on cloud physicists, crystallographers and meteorologists.

The question is thus not: are all crystals different, but rather has there been any case that people found 2 identical crystals? And if not, is there any proof that they can't be identical?

Sklivvz
  • 78,578
  • 29
  • 321
  • 428
Terry
  • 660
  • 4
  • 11
  • 2
    There's no a-priori reason why they can't be identical. It's not that the shapes get written down in a cosmic register and a snow flake in Aspen checks if there was, 100 years ago, a snow flake in Hokkaido that had the same shape. It's just *very* improbable. – Lagerbaer Apr 19 '11 at 15:06
  • 1
    Is it possible that two snow crystals are exactly alike? Yes, sure! It's just VERY unlikely! – Martin Scharrer Apr 19 '11 at 15:20
  • @Lagerbaer - in other words, `Snow crystal = GUID`? – Nicole Apr 19 '11 at 17:39
  • Of course we have to define identical really. Is one molecule more or less, or organized differently, enough to quantify as not identical? If so... I might suggest no things we ever see are identical??? – JeopardyTempest Aug 06 '18 at 07:03

2 Answers2

10

This is too long to fit in a comment on Oliver_C's answer, so it's getting its own answer. Let's assume Professor Libbrecht's analysis is correct and there are 10158 possible snowflake configurations. Roughly 1023 snow crystals fall on Earth per year.

If 1023 snow flakes fall per year, then by the pigeonhole principle two similar flakes must fall by the time the Earth reaches the age 10158/1023 = 10135 years, which isn't going to happen any time soon.

With that said...

Now lets assume that each one of the 10158 possible snowflake configurations is equiprobable (I am not sure if this is a reasonable assumption, but let's proceed). If there are n possible types of snowflake and i-1 < n snowflakes have fallen, the probability that the i th snowflake is different is (n - (i - 1))/n. Therefore, if k snowflakes have fallen, then the probability that they are all different is the product of (n - (i - 1))/n for i ranging from 1 to k. Since n and k are positive, this simplifies to (-1)k n-k (-n)k , where "(x)n" denotes the Pochhammer symbol. Plugging in 10158 for n and 1023t for k, we arrive at

(-1)1023t (10158)-1023t (-10158)1023t .

This is the probability that t years of snowfall of 1023 flakes/year drawn uniformly from a set of 10158 possible flake configurations has produced no duplicate flakes. Even plugging in t = 1 produces an underflow error on all of the numerical analysis systems I've used (is anyone else able to calculate the result?), which should tell you that the probability of all flakes being different even in a single year is very low. The age of the Earth is roughly 4.54 billion years.

Update:

So, after thinking about this for a while, I realized that this is all just an instance of the Birthday Problem: The problem is exactly the same as finding the probability that at least two people share a birthday in a room full of 4.54x109x1023 people when there are 10158 possible birthdays. There are well known approximations for calculating this probability, which result in a value incredibly close to zero. The derivation is a bit long and math-laden, so I posted it on my website if you are interested. Therefore, if the configurations of snowflakes are uniformly distributed, then there is an extremely low probability that any two snowflakes have been similar in the history of the Earth.

But wait! Do snowflakes really occur according to a uniform distribution? I'd imagine that some configurations are more rare than others. Like many other natural phenomena, I might guess that the distribution of configurations is closer to a Zipfian (a.k.a. "Power Law") distribution. Using this distribution unfortunately forces us to abandon the handy approximation that we used in the uniform case; we'll have to derive the probability from scratch. The probability that among n snowflakes at least two are the same is this nasty expression:

1 - 1/n! sum_{x1=1}^{10158} sum_{x2=x1+1}^{10158} sum_{x3=x2+1}^{10158} ... sum_{xn=xn-1+1}^{10158} product_{i=1}^n xi-2 / sum_{j=1}^k j-2.

(For a prettier representation in MathJax, along with additional steps in the derivation, see my website.)

This expression can be bounded below by 1 - 10158 / n! ζ(2)n. Setting n = 1023, this lower bound is extremely close to 1. Therefore, if the snowflakes are configured according to a Zipfian distribution, there is a very high probability that at least two snowflakes are similar in a single year! The same applies if the snowflakes are binomially distributed (that derivation is also on my website).

Community
  • 1
ESultanik
  • 8,038
  • 3
  • 38
  • 49
  • 3
    The probability doesn't need to be summed. If p is the probability that two snowflakes are alike, and n the number of snowflakes, and p is almost zero (1E-158), we can disregard the possibility of more than one match. The number of pairs to examine is n(n +1)/2, which is close enough to n^2/2. Plugging in, we get 1E46/2 = 5E45 pairs a year, so (1 - 1E-158)^5E45 is the probability of two matches per year, which is going to be hard to calculate. 1E-158 * 5E45 will be close enough, then, which is 5E-113. This leaves 5E-113 * 5E9 = 2.5E-103 for the approximate probability of twins. – David Thornley Apr 20 '11 at 00:57
  • @David +1 for your approximation. If the distribution of flake configurations is normally distributed as is suggested in the other answer, that should increase the probably that two flakes are similar. – ESultanik Apr 20 '11 at 14:00
  • @ESultanik: Nice answer! Two things: 1. Before the update you write "the probability of all flakes being different even in a single year is very low", then in the update you say "there is an extremely low probability that any two snowflakes have been similar in the history of the Earth" - this looks rather contradictory to me. 2. In your blog, you write "if there are at least 365 people in the room then there must be at least one pair of people that share a birthday". You means _366_ (or even _367_ if you want to allow for leap years). – Hendrik Vogt Sep 07 '11 at 14:04
  • @Hendrik: Good points. 1. I think I actually have an error (either typographical or mathematical) in my previous analysis (it's been a while since I first wrote it); I am going to redact that text because it is superseded by the new analysis. 2. Good point, I'll mention that. – ESultanik Sep 07 '11 at 14:18
  • @Esultanik: `:-)` – Hendrik Vogt Sep 07 '11 at 14:40
9

From Kenneth Libbrecht (Professor of Physics, Caltech)

The number of possible ways of making a complex snowflake is staggeringly large.

To see just how much so, consider a simpler question:
how many ways can you arrange 15 books on your bookshelf?

Well, there's 15 choices for the first book, 14 for the second, 13 for the third, etc.

Multiply it out: 15 * 14* 13 * ...

... and there are over a trillion ways to arrange just 15 books.

With a hundred books, the number of possible arrangements goes up to just under
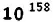enter image description here(that's a 1 followed by 158 zeros).

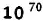That number is about enter image description here times larger than the total number of atoms in the entire universe!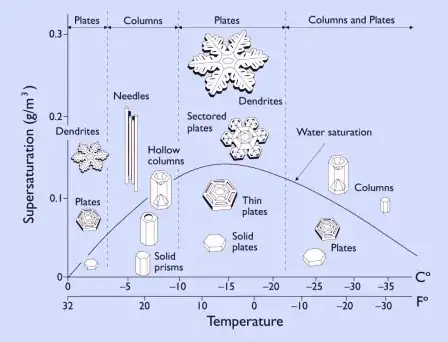

Now when you look at a complex snow crystal, you can often pick out a hundred separate features if you look closely. Since all those features could have grown differently, or ended up in slightly different places, the math is similar to that with the books.

Thus the number of ways to make a complex snow crystal is absolutely huge. And thus it's unlikely that any two complex snow crystals, out of all those made over the entire history of the planet, have ever looked completely alike.

So, in theory two (or more) snowflakes can look alike, but the probability is incredibly small.

(This is similar to humans and their fingerprints)

Snowflakes (Image Source)

The shapes of snowflakes depend on the temperature and humidity.

Community
  • 1
Oliver_C
  • 47,851
  • 18
  • 213
  • 208
  • 1
    The [cited source](http://www.highbeam.com/doc/1P2-8066647.html) is behind a paywall, but according to [Wikipedia](http://en.wikipedia.org/wiki/Snowflake#Uniqueness), two alike snowflakes *were* found in Wisconsin in 1988. – Jason Plank Apr 19 '11 at 16:44
  • [here](http://www.windows2universe.org/earth/polar/cryosphere_snow2.html) is a photo of those two alike snowflakes – Oliver_C Apr 19 '11 at 17:05
  • 10
    The pictured argument contradicts your theoretical claims, which brings us closer to what I believe the truth to be. The shape of a snowflake is likely determined by many factors, not completely random but living on a normal distribution. Arranging a bookshelf isn't a random process for most people, as we tend to alphabetize, or group preferred books first. It would not be unreasonable to see two people with similar interests group a small number of books the same way. Just because I don't know how a snowflake decides how to look does not mean the process is completely random. – Joshua Shane Liberman Apr 19 '11 at 17:20
  • @Joshua- I agree, the growth is not 'random'. Two snowflakes growing under exactly the same conditions should look exactly alike. The question is, how sensitive is the growth to change in temperature and humidity? Would a difference in conditions of say 0.001% already lead to a visibly different growth pattern? – Oliver_C Apr 19 '11 at 17:49
  • 3
    10^158 is a huge underestimate. A typical snowflake contains 1 X 10^20 water molecules. [hypertextbook](http://hypertextbook.com/facts/2001/JudyMoy.shtml) It is the relative positions of all those that must all be identical, not some 100 arbitrary large scale features. That number merely serves to show how quickly the improbability of identity grows with an increasing number of occupiable states. –  Apr 19 '11 at 22:47
  • 1
    @Jason @Oliver That sighting / photo can almost certainly be discarded as fake. The probability is just too small. In fact, “too small” is entirely misleading. With such huge numbers, the probability is, for all intents and purposes, non-existent. Or, put differently: the probability of observing two identical snowflakes is unthinkably smaller than the probability of a fake. – Konrad Rudolph Apr 20 '11 at 08:44
  • 6
    The thing with that photo is that they're *similar*, not *identical*. You could say that any two snowflakes are "alike" when using a loose enough definition. You could also say that no two snowflakes are identical with a strict enough definition. – Ezra Apr 20 '11 at 09:25