Fingerprints are often used by law enforcement to identify individuals, even with a partial print. Are there any cases where people had the same fingerprints? Is there a limit to the number of unique fingerprints that can possibly exist?
-
@ChrisW Saw that question but it relates more to possible human errors and other factors when processing fingerprints, so I thought this deserved it's own question – msmucker0527 Aug 28 '14 at 18:07
1 Answers
In theory, no, but the odds for it happening are really low.
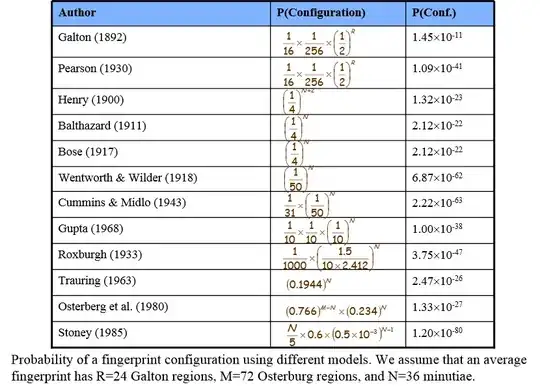
This presentation has a slide with an overview of the literature on the subject. If I'm interpreting the chart copied below, estimations of the possible configurations of fingerprints (i.e. the probability of a given fingerprint occurring) range from 1.45x10-11 to 1.20x10-80. Given that the number of people who have ever lived is estimated to be 100 billion to 115 billion (1.15x1011), then it's mathematically possible for every human who ever lived to have unique fingerprints.
 Since there's nothing which hands out fingerprints and ensures uniqueness, it's quite possible that there have been duplicates at some point. However, the odds for duplicates actually coming up in a real world scenario (i.e. two people living in the same country within the same general span of time, instead of anywhere in the world at any point in history) are infinitesimal.
Since there's nothing which hands out fingerprints and ensures uniqueness, it's quite possible that there have been duplicates at some point. However, the odds for duplicates actually coming up in a real world scenario (i.e. two people living in the same country within the same general span of time, instead of anywhere in the world at any point in history) are infinitesimal.
Added to address comments: It's worth noting that all these probabilities are based on the granularity of the method involved. The Galton method, for instance, seems to involve dividing the finger up into 24 regions, and identifying the most prominent feature of that region. This leads to a fairly granular set of results, which, in turn, means that it's much easier to find someone else who would register as having the same set of fingerprints. This would be roughly equivalent to a version of the birthday problem where you're trying to find people who have the same birth month, instead of the same birthday.
Modern matching systems use the minutia of the fingerprint to provide a much more accurate match. My understanding of it is that there are 36 points selected based on finding certain features in a general area (i.e. five points of interest in this small section), and the precise relative location of each point to each other is what makes up the modern fingerprint record. This produces a far more accurate digital record of the fingerprint, although still not a 100% perfect one. Correspondingly, this makes the chances of finding two fingerprints considered to be a match much lower. To extend the previous analogy, you're now trying to find two people who share a birth minute, not just a birth day.
- 3,086
- 26
- 28
-
1This begs the question of how similar two "different" fingerprints might be. Are we talking about differences you could see with the naked eye, or microscopic differences? Also as a point of interest, if Galton were right, then it only takes around 400K people to get a 50-50 shot of two people having the same fingerprint, meaning it would be very unlikely for there NOT to be two people in the US with identical fingerprints. – Rob Watts Aug 28 '14 at 22:56
-
1@RobWatts - The presentation I linked to goes into somewhat more detail, although it's obviously meant to accompany a talk. I did [a bit more reading](http://books.google.com/books?id=duUJEp4WbQ8C&pg=PA335&lpg=PA335&dq=galton+regions&source=bl&ots=Hj3wXY51JR&sig=w2zz-HLHe5nScS4USx_jNWbp8fY&hl=en&sa=X&ei=nIYAVMyEOtDLggSZ44HQCg&ved=0CCcQ6AEwAQ#v=onepage&q=galton%20regions&f=false) and basically, Galton's method isn't considered very accurate. The "minutiae" method uses each ridge split or join, which is more precise and what most use today (I think). – Bobson Aug 29 '14 at 14:03
-
@Bobson: You oversaw the problem of the [birthday paradox](http://en.wikipedia.org/wiki/Birthday_problem). If we assume a fair distribution each fingerprint occupies randomly one slot. The birthday paradox approximately increases the probability squarely with the number of people involved (Halmos upper bound for p=50%: sqrt(2*N*ln(2)). If N = 10e11 then a duplicate is to expected with 370 000 people ! Given the number of people on earth we need at least a probability of 1/2.59e19 which is much more than expected. Galton will lead to a duplicate, Henry, Balthazar and Bose are possible. – Aug 31 '14 at 19:19
-
@ThorstenS. - Since you're the second person to mention that, I edited the answer to address it. Basically, Galton's method was the very first, and isn't in use today for precisely that reason. – Bobson Sep 02 '14 at 05:20
-
Is there any reason to believe that Stoney's 10^80 "possible fingerprints" are anywhere close to being equally probable? If two people were to each flip 1,000 coins, there would be 1,001 different values for the number of heads each person flips, but the probability of two both people flipping the same number of heads would be much greater than 1/1,000. – supercat Sep 05 '14 at 23:36
-
@supercat - Honestly, I have no idea. My default assumption from some of the diagrams I was looking at were that each part was pretty independent (and thus each fingerprint is equally probable), but I didn't find anything specifically stating one way or the other. Feel free to dig into it a bit more, if you're curious. – Bobson Sep 07 '14 at 22:01
-
@Bobson: The figures you cite make it sound as though the probability of two randomly-selected people having a Stoney match would be about 1/10^80; I was wondering if that claim had any real statistical basis beyond a hope that the variables aren't so biased as to make the probability high enough to matter. – supercat Sep 08 '14 at 15:45
-
@supercat - Check out [this paper](http://www.ee.nthu.edu.tw/whhsu/homework/hw_4.pdf) - it discusses Stoney's model (among others) in much greater detail than I've seen elsewhere. At a *very* brief skim, it seems that his model specifically does take into account that certain features are more likely to be near other ones. – Bobson Sep 08 '14 at 16:54
-
Not that it matters, but the "birthday collision" mistake is being made here. – Fattie Dec 31 '17 at 18:54
-
-
hey @Bobson, happy new year; sorry I just glanced over the discussion and was not addressing you in particular. Consider a group of people (365 possible birthdays). For there to be a 50% probability of a collision, surprisingly **you only need twenty-three people**, not (as one would assume without analyzing it) 360 or 180 people. This surprising statistical result has already been mentioned in other comments. Cheers! – Fattie Jan 01 '18 at 16:08