It is very hard to prove they can't have 4-fold symmetry but we have a good understanding of why they usually have 6-fold symmetry under normal conditions.
The structure of snowflakes is driven by the underlying symmetry of ice at temperatures near zero Celsius (or whatever that is in non-standard american units) and pressures close to atmospheric. The crystal structures at high pressures or extreme temperatures can be different (Ice IX, for example, has a tetragonal crystal structure so might form crystals with a four fold symmetry, but it it is only stable at low temperatures and high pressures, thank goodness).
The underlying structure that drives six-fold symmetry in normal ice looks like this:
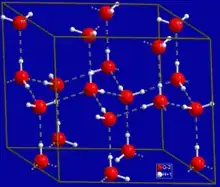
with the symmetry arising because of the way water molecules hydrogen bond to each other in networks.
As Kenneth Libbrecht's fantastic article (NB pdf) on snowflakes explains:
The angle between atoms in a water molecule mandates a hexagonally shaped ice lattice, which ultimately leads to the snowflake’s sixfold symmetry. As a result, snow crystals first develop into small, faceted prisms, which may grow to a few tenths of a millimeter in size, about as large as the period at the end of this sentence. Depending on the details of how they grow, these simple crystals may become slender hexagonal columns shaped like wooden pencils, thin hexagonal plates, or anything in between.
The article is well worth reading not only for its wide range of pictures of snowflakes but for an extend discussion on the factors that create such a variety of six-fold shapes.
