Is Earth as smooth as a billiard ball?

Question

I've heard it said (on the YouTube channel vsauce) that the earth is smoother than a billiards ball if it's scaled down.

Is this true?

Of course the earth is relatively smooth:

Mt. Everest: ~10km+
Mariana Trench: ~13km-
Earth's Diameter: 12,750km

But a billiards ball feels as smooth as a mirror!

to a hand scaled up accordingly, the earth would feel as smooth as a mirror :-) — Rory Alsop, Sep 06 '12 at 08:17
In [this site](http://billiards.colostate.edu/threads/balls.html#magnified) you can find a picture of a billiard ball, very magnified. It seems that the deeper points go below the shown scale, and the peaks also go above it. Ok. But the scale is in the micron-resolution... — woliveirajr, Sep 06 '12 at 12:21
In related research comparing the earth's surface to things that lack variation, [Kansas is considerably flatter than a pancake](http://www.improbable.com/airchives/paperair/volume9/v9i3/kansas.html). I would actually have expected both memes to arrive at the same result (earth's surface flatter in both cases or vice versa). — csfowler, Sep 06 '12 at 20:13
define smooth. one is little deviation from the average height (the one used by the vid) another is that the microfacets don't exceed a certain gradient (which makes something shiny) — ratchet freak, Sep 07 '12 at 22:22
This article analyses billiard balls again and compares with the Earth surface: http://billiards.colostate.edu/bd_articles/2013/june13.pdf — woliveirajr, Sep 20 '13 at 19:52
http://www.improbable.com/airchives/paperair/volume9/v9i3/kansas.html shows conclusively that Kansas is more smooth than a pancake. Not exactly what you're asking for but helps explain why the claim is ridiculous. — jwenting, Sep 21 '13 at 07:36
Related What if? article: [Bowling Ball](https://what-if.xkcd.com/46/) — Tomáš Zato, Feb 16 '16 at 14:16

score 86 · Accepted Answer · edited Jun 17 '20 at 09:41

86

This strongly depends on definition of what smoothness is.

The Discover Magazine blog addressed this in 2008

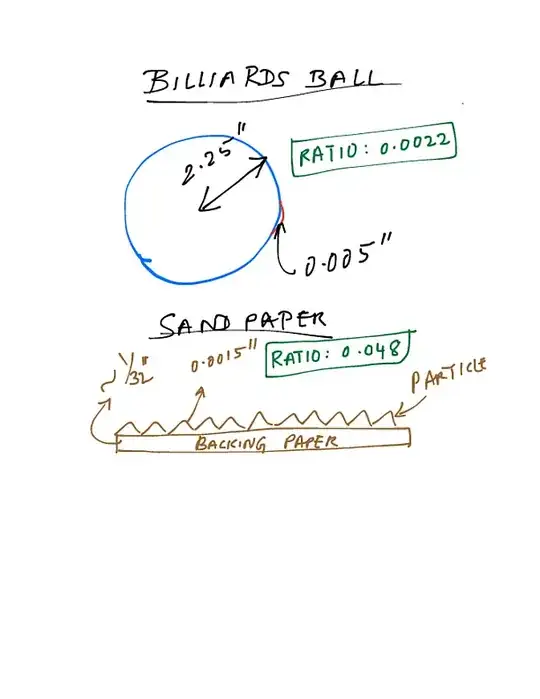
OK, first, how smooth is a billiard ball? According to the World Pool-Billiard Association, a pool ball is 2.25 inches in diameter, and has a tolerance of +/- 0.005 inches. In other words, it must have no pits or bumps more than 0.005 inches in height. That’s pretty smooth. The ratio of the size of an allowable bump to the size of the ball is 0.005/2.25 = about 0.002.

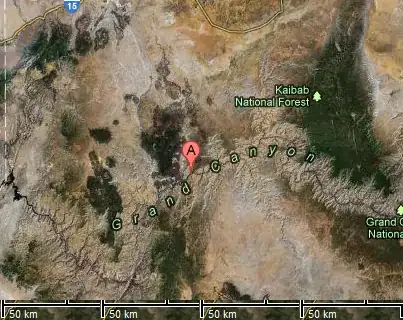
The Earth has a diameter of about 12,735 kilometers (on average, see below for more on this). Using the smoothness ratio from above, the Earth would be an acceptable pool ball if it had no bumps (mountains) or pits (trenches) more than 12,735 km x 0.00222 = about 28 km in size.

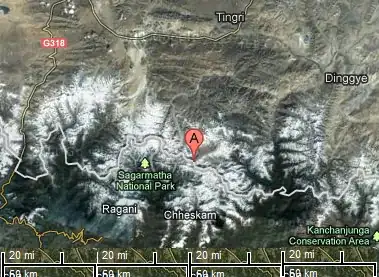
The highest point on Earth is the top of Mt. Everest, at 8.85 km. The deepest point on Earth is the Marianas Trench, at about 11 km deep.

Hey, those are within the tolerances! So for once, an urban legend is correct. If you shrank the Earth down to the size of a billiard ball, it would be smoother.

I disagree with definition of smoothness used by Discovery Magazine. By that definition, medium sandpaper (grit particle size of 0.005 in) is also smooth, which doesn't quite go with my definition of smoothness. In fact I find claim that sandpaper is smooth to be ridiculous.

With mountains reaching in excess of 8,000m, scaled down that would be 0.0015 in. which means, that scaled down Earth's "smoothness" is equivalent to that of 320 grit sandpaper.

enter image description here

How does it compare with actual billiard ball, woliveirajr's answer is helpful:

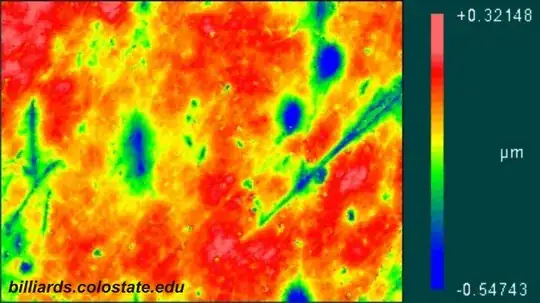
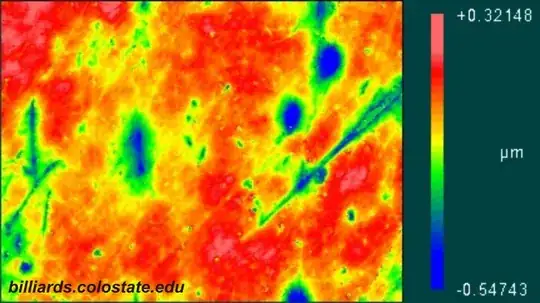
What does ball surface look like: enter image description here

enter image description here

Note, that variation is about 0.55μm, while 0.005 inches official tolerance for shape is 127μm. 0.55μm scaled up to Earth size would be less than 125 meters.

As for shape, which is really what the ±0.005 inches regulation is about, Earth is non-spherical, it's oblate spheroid with:

Equatorial radius: 6,378.1370 km
Polar radius: 6,356.7523 km
Mean radius: 6,371.009 km (sources: WGS-84 and IUGG )

Just the non-spherical shape already disqualifies scaled down Earth as official billiard ball, allowable tolerance in diameter would be 28,326 m while difference between Earth's polar diameter and mean diameter is 28,513 m. Although it is quite close call.

edited Jun 17 '20 at 09:41

Community

1

answered Sep 06 '12 at 10:16

vartec

26,581
5
97
155

If the tolerance is __"+/- 0.005 inch"__ then you have a total tolerance of __"0.01 inch"__. This would allow the Earth's diameter to vary by 56km (instead of 28km). – Oliver_C Sep 06 '12 at 10:50
@Oliver_C: no, sorry, but that's wrong; "+/- 0.005 inch" is 0.005 inch above or below **average**. It does allow up to 0.01 inch difference between bump and dip though. But I'm not comparing polar diameter with equatorial one, but polar diameter with average one. – vartec Sep 06 '12 at 10:53
1

You are right, the difference between "Mean" and "Polar" is slightly above "0.005". But if one looks at "Equatorial" (longest) and "Polar" (shortest) diameter, the difference is 48km. This would fall within the "0.01" total variance (56km). – Oliver_C Sep 06 '12 at 11:38
20

Bah non-spherical doesn't disqualify it at all. The question was about smoothness, not about shape. – hippietrail Sep 06 '12 at 11:56
@hippietrail: but +/- 0.005 inches tolerance is about shape – vartec Sep 06 '12 at 12:02
6

@vartec that means **your** definition of smoothness would only work for spheres. But smoothness is _having a texture that lacks friction_ which is a property of the surface not of the underlying shape. – Stefan Sep 06 '12 at 12:16
2

@Stefan: you mean the definition, that prepended with words "I disagree with"? :-P – vartec Sep 06 '12 at 12:19
14

@Stefan, it's Discovery Magazine's definition of smoothness, not vartec's (nor the WBPA's). The [actual spec](http://www.wpa-pool.com/web/WPA_Tournament_Table_Equipment_Specifications) says "All balls must be composed of cast phenolic resin plastic and measure 2 ¼ (+.005) inches [5.715 cm (+ .127 mm)] in diameter". Since it's talking about _diameter_, this specification is about deviation from spherical shape. So Discovery Magazine made _two_ mistakes. 1) The earth does _not_ meet the specification. 2) The specification has nothing to do with smoothness, in the everyday sense. – senderle Sep 06 '12 at 13:46
Actually, reading the DM blog post itself, they do address a lot of these nuances. In fact, they directly address the difference between shape and surface, and they seem to disagree with my interpretation of the spec -- they think it's about surface and _not_ necessarily about roundness at all: "Of course, that’s assuming the tolerance for being out-of-round for a billiard ball is the same as it is for pits and bumps. The WPA site doesn’t say. I guess some things remain a mystery." So I have to take back the above comment, at least partially. – senderle Sep 06 '12 at 14:11
@vartec: 29 up-votes in 7 hours, and I am forced to agree with you that your answer is better. [Sob.] Would you like to make your answer stand-alone and directly referencing the argument you are refuting, so I can delete mine. [Sob.] – Oddthinking Sep 06 '12 at 14:54
@vartec I think i see your point (with the updated answer). They used the wrong figure to describe the smoothness. As you say **"As for shape, which is really what the ±0.005 inches regulation is about"**. The question is then is there even a spec for smoothness of the balls or is it just shape related? Because if not one could legally make those with a sandpaper cover. And +1 for the updated and much better answer. – Stefan Sep 06 '12 at 15:05
2

@Oddthinking: done, however if I were you, I'd leave yours for reference. – vartec Sep 06 '12 at 15:17
I withdraw my complaint after your effective work at re-wording your answer - thanks (-: – hippietrail Sep 06 '12 at 16:47
Does this answer actually answer the quesiton? From what I'm reading, according to Discovery magazine's criteria for smoothness, the earth would be as smooth as a billiard-ball, but also as smooth as sandpaper, which is clearly absurd. But, the answer doesn't give an alternate definition of smoothness to actually answer the question. The "smoothness" should take into consideration not the change in height, but the rate at which the height changes... – BlueRaja - Danny Pflughoeft Sep 07 '12 at 19:15
Also, regulating a a tolerance on the diameter of the ball is not the same as regulating its smoothness. You could have a ball with tolerance 0.55μm that is still as coarse as sandpaper. This entire answer is just misdirection. – BlueRaja - Danny Pflughoeft Sep 07 '12 at 19:22
For example, [here](http://i.imgur.com/tLvqr.png) is an incredibly well-drawn *(if I do say so myself)* zoomed-in side-view of two surfaces. They both have the same change in height over the same area, but one will be coarse while the other is smooth. So the question is really: is the earth's surface mostly coarse, like the left image, or smooth, like the right? Determining the difference in height will not tell you that *(it is possible for [an object to have widely varying heights](http://goo.gl/UHMUl) and still be smooth, as long as the changes are very gradual)*. – BlueRaja - Danny Pflughoeft Sep 07 '12 at 21:41
@BlueRaja: clearly in case of Himalayas and Andes it's not gradual. – vartec Sep 09 '12 at 20:38
This answer is simply wrong. The mistake is in fixating on the "mean" diameter, which as you may notice isn't even the mean in the usual arithmetic sense. Based on the given polar and equatorial radii, the Earth's radius deviates by +/- 10.69235 m from a perfect sphere of radius 6367.44465 m. Scaled to a diameter of 2.25 in, this is a deviation of only +/- 0.0037 in. – Kevin Krumwiede Oct 17 '18 at 07:10

score 19 · Answer 2 · answered Sep 06 '12 at 15:37

I think vartec has the best answer so far. The quoted tolerance (specifications link) of 0.005 is for total size, not smoothness. The spec says 2.25+.005, not +/-, is that a typo or does it mean the balls must be at least 2.25 but not more than 2.255"? Most balls are actually manufactured to a higher tolerance, with good ones being under 0.001".

The pic from the site woliveirajr found is shows 1mm of an actual ball. That equates to about 220 km on the surface of the Earth, here's the pic compared to part of the grand canyon and everest:

enter image description here Grand Canyon (200km)

And while the scaled-down grand canyon would be 8.2 micrometers deep, the variation in the marks is less than 1 micrometer (about 0.87).

enter image description here

So while I've seen billiard balls with scratches and chips that might be larger than mountains on Earth might be at that scale, that is not what you think of when you think of how smooth a billiard ball is.

Everest is different than the Grand Canyon though, Mount McKinley in Alaska is actually taller base-to-peak as Everest has a higher base. So while Everest would rise to a point further from the center of the billiard ball, Mount McKinley would be the highest bump at about 26 micrometers from the surrounding surface.

I don't compare Mauna Kea because I would argue that under sea level should not be taken into account. After all, looking at the Earth from space, you cannot see the Mariana Trench. You run into all sorts of problems thinking about a giant being trying to feel how smooth the Earth is, so I would just just use how it looks from space, water or not:

Giant fingers touching it would be like moons or huge asteroids impacting the surface.
In any gravity field that would drain the water, resting the earth on a surface or holding it would make it collapse, releasing the molten core and causing enough friction to turn the rest molten as well
Water molecules would be about 5" big on the scaled down earth. It would not act much differently from rock at that scale.

60 foot Ocean waves would be about 0.08 microns, but as that is far from the norm and waves would be so tightly packed that they would seem to be almost one surface, most of the planet would be much smoother than a billiard ball. Much of the rest of the world would be about as smooth as well, it would just be the large mountain ranges that would really be much rougher.

Also what would happen with all the water if you gave the earth a good Force follow. http://en.wikipedia.org/wiki/Cue_sports_techniques#Force-follow — Captain Giraffe, Sep 06 '12 at 18:02
if you're referencing relative height, Nanga Parbat is taller (7000m relative height) than Mt McKinley (5900m relative height). — vartec, Sep 07 '12 at 10:35

score 2 · Answer 3 · edited Sep 07 '12 at 06:53

2

I'm sorry to rain on vartec's parade, but his answer is conceptually incorrect and falls into the fallacy of comparing apples and oranges and tries to appeal to familiarity with every day objects to make the case (incorrectly). The quoted article is correct (of course, requires one to make the assumption that the earth is round, which is not a terrible assumption for the purposes of the article) and below, I offer a reasoning of why vartec's answer is grossly misleading.

To understand why, one should understand dimensional comparisons. The billiards ball example compared the maximum bump to the radius (or diameter). Both these directions are comparable. As the quoted article shows, doing the same for the "bumps" on the Earth led to a smaller ratio of max bump size to radius and hence "smoother".

Now the part that's misleading (and upon which the rest of the argument is based) is that scaling this down to "normal size" makes it comparable to sand paper! How? How is this scaling done? To scale properly, one would have to take the dimensionless ratio of bump size to radius (see crude figure below) of the billiard ball (or the Earth) and then multiply it by the corresponding dimension of another object you wish to compare. This dimensionless ratio is the definition of "smoothness" (0.0022 in the image), not the actual number 0.005".

In the comparison with the sand paper, he "scales" Mt.Everest down to 0.0015 inches. How was this "rescaling" done? What is the base line that this is a "deviation" from? He doesn't tell you. And this is where the mistake lies. In the second half of my crude hand drawn image, I give an example. Let's assume that 0.0015 grit size sand paper is chosen. We now need to consider the dimension for which this grit can be considered a "bump". No, it's not the length, but the thickness of the backing paper that matters. Let's now assume a thickness of 1/32" (don't know the actual number, but somewhere between 1/32" and 1/16" is my guess). Calculate the dimensionless "smoothness" factor again – turns out it is 0.048, which is much greater than 0.0022. Well, duh! No wonder it is rough — it is about 20 times rougher, in fact.

If you've ever worked on auto detailing, you might have come across 2500 grit sand paper. These are very smooth to the touch (seriously, smooth as talc), and still they're about 5 times rougher than a billiards ball.

So in summary, the entire answer is based on false math and I'm concerned that it has as many as 50+ votes on a Skeptics site.

edited Sep 07 '12 at 06:53

Henry

13,472
1
54
62

answered Sep 07 '12 at 05:04

12

so you're basically saying, that the thicker the paper backing sandpaper's surface, the smoother it is? – vartec Sep 07 '12 at 10:41
2

It is ridiculous to claim that the thickness of the paper is the measure of roughness. The claims in this answer are baseless, unsupported by any reference. – Sep 07 '12 at 11:05
They used the wrong number the 0.005 is not the definition for the smoothness but for the deviation from a sphere. A mirror would be very smooth but does deviate more than 0.005 inches from a sphere (with a certain diameter) it is therefore a bad billiard ball. Since they are using the wrong number it cannot be used for smoothness calculation. – Stefan Sep 07 '12 at 22:00
1

@vartec, if you remember, the question is about scaling everything to the same size and _then_ comparing their smoothness. So yes, the more you increase the thickness of the backing paper, the smaller the particles become after scaling and thus it becomes smoother. This is the same reason why Earth with 8Km high mountains still feels smooth after scaling down. – Shahbaz Sep 09 '12 at 09:30
1

@Shahbaz But it wouldn’t feel smooth. Mt Everest would stand out on your billard ball Earth like a grain of sand on sandpaper. The thickness of the paper is totally irrelevant for that. You can mount sandpaper to a piece of wood (= thicker backing) without influencing its sanding property in the slightest. – Konrad Rudolph Sep 10 '12 at 10:41
1

@KonradRudolph, if you stick the sandpaper on earth itself, and scale it down to a billiard ball would you still feel it? Obviously not. If you stick the sand paper on a piece of wood and scale it down to the size of a sand "paper", it feels it feels less rough. I don't know what effect mount everest would have on the smoothness of earth, but I am merely saying that, as this answer also says, the top answer has a wrong logic. – Shahbaz Sep 10 '12 at 11:55
3

@Shahbaz Totally irrelevant. We don’t scale the sandpaper down. We are using it as a comparison, because Mt Everest, on a billiard ball sized Earth, would have the size of a grain of sand on *regular* sandpaper. Thus a billiard sized Earth would feel like regular (non-scaled!) sandpaper. – Konrad Rudolph Sep 10 '12 at 12:02
@KonradRudolph, I see now what you mean. I had missed the line in that post where it says "0.0015" is the same as a "320 grit sandpaper". – Shahbaz Sep 10 '12 at 12:41
I don't understand why the thickness of the paper would change the smoothness of a surface – Django Reinhardt Oct 03 '22 at 19:24

Is Earth as smooth as a billiard ball?

3 Answers3