The Birthday Paradox is a phenomenon in probability in which the probability of a population containing two individuals with the same property is much greater than would be intuitively expected. In its original form it describes the likelihood that any two individuals in a room share a birthday. Amongst other things, the Birthday Paradox affects cryptography, hashing and various applications of random number generators.
The Birthday Paradox is a phenomenon where two individual samples selected from a population may have the same value, for example the birthdays of individuals in a room. The paradox is that the probability of this coincidence happening is much higher than people expect. Amongst other things the phenomenon affects hashing, cryptography and various applications of random number generators.
Overview
The problem is originally defined as the probability of any two people in the room sharing the same birthday. The key point is that any two people in the room could share a birthday. People tend to naively misinterpret the problem as the probability of someone in the room sharing a birthday with a specific individual, which is the source of the cognitive bias that often causes people to underestimate the probability. This is the incorrect assumption – there is no requirement for the match to be to a specific individual and any two individuals could match.
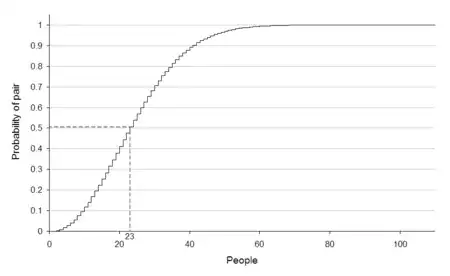
The probability of a match occurring between any two individuals is much higher than the probability of a match to a specific individual as the match does not have to be to a specific date. Rather, you only have to find two individuals that share the same birthday. From this graph (which can be found on the wikipedia page on the subject), we can see that we only need 23 people in the room for there to be a 50% chance of finding two that match in this way.
Some applications
Cryptographic hashing relies on the low probability of any two items having the same hash value. In order to achieve this the hash value must be very large so as to make it computationally infeasible to find another item that hashes to the same value. The Birthday paradox means that the width of the hash values must be very large in order for the probability of a collision to be sufficiently low.
In a Hash Table, the Birthday Paradox makes the likelihood of collisions quite high unless you have a perfect hash function that hashes a controlled set of source values to a unique set of hash values. In other cases, the hash table must be able to deal with relatively frequent collisions.
If you need a guaranteed unique sequence of random numbers, you cannot rely on simply generating random numbers, as the probability of a collision is quite high for relatively small sample sets. Instead, a set of unique numbers must be generated (perhaps just sequentially) and shuffled into a random order.
The tag is most applicable to questions about applications directly affected by the phenomenon (e.g. cryptographic hashing), or perhaps re-tagging a question where the poster has displayed obvious naievity about it.