Projection onto unit simplex using gradient decent in Pytorch

Question

In Professor Boyd homework solution for projection onto the unit simplex, he winds up with the following equation:

g_of_nu = (1/2)*torch.norm(-relu(-(x-nu)))**2 + nu*(torch.sum(x) -1) - x.size()[0]*nu**2 

If one calculates nu*, then the projection to unit simplex would be y*=relu(x-nu*1).

What he suggests is to find the maximizer of g_of_nu. Since g_of_nu is strictly concave, I multiply it by a negative sign (f_of_nu) and find its global minimizer using gradient descent.

---

Question

My final vector y*, does not add up to one, what am I doing wrong?

---

Code for replication

torch.manual_seed(1)
x = torch.randn(10)#.view(-1, 1)
x_list = x.tolist()
print(list(map(lambda x: round(x, 4), x_list)))
nu_0 = torch.tensor(0., requires_grad = True)
nu = nu_0
optimizer = torch.optim.SGD([nu], lr=1e-1)

nu_old = torch.tensor(float('inf'))
steps = 100
eps = 1e-6
i = 1
while torch.norm(nu_old-nu) > eps:
  nu_old = nu.clone()
  optimizer.zero_grad()
  f_of_nu = -( (1/2)*torch.norm(-relu(-(x-nu)))**2 + nu*(torch.sum(x) -1) - x.size()[0]*nu**2 )
  f_of_nu.backward()
  optimizer.step()
  print(f'At step {i+1:2} the function value is {f_of_nu.item(): 1.4f} and nu={nu: 0.4f}' )
  i += 1
y_star = relu(x-nu).cpu().detach()
print(list(map(lambda x: round(x, 4), y_star.tolist())))
print(y_star.sum())

[0.6614, 0.2669, 0.0617, 0.6213, -0.4519, -0.1661, -1.5228, 0.3817, -1.0276, -0.5631]
At step  1 the function value is -1.9618 and nu= 0.0993
.
.
.
At step 14 the function value is -1.9947 and nu= 0.0665
[0.5948, 0.2004, 0.0, 0.5548, 0.0, 0.0, 0.0, 0.3152, 0.0, 0.0]
tensor(1.6652)

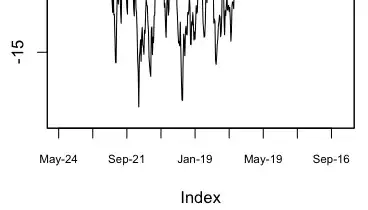
The function

torch.manual_seed(1)
x = torch.randn(10)
nu = torch.linspace(-1, 1, steps=10000)

f = lambda x, nu: -( (1/2)*torch.norm(-relu(-(x-nu)))**2 + nu*(torch.sum(x) -1) - x.size()[0]*nu**2 )

f_value_list = np.asarray( [f(x, i) for i in nu.tolist()] )

i_min = np.argmin(f_value_list)
print(nu[i_min])

fig, ax = plt.subplots()

ax.plot(nu.cpu().detach().numpy(), f_value_list);

Here is the minimizer from the graph which is consistent with the gradient descent.

tensor(0.0665)

Answer 1

The error comes from the derivation of the formula:

from:

If you develop the expression

you will realize that it should be

instead of

In short, this error comes from forgetting the 1/2 factor while developing the norm. Once you make that change everything works as intended:

import torch
import torchvision
import numpy as np
import matplotlib.pyplot as plt

torch.manual_seed(1)
x = torch.randn(10)

x_list = x.tolist()

nu_0 = torch.tensor(0., requires_grad = True)
nu = nu_0
optimizer = torch.optim.SGD([nu], lr=1e-1)

nu_old = torch.tensor(float('inf'))
steps = 100
eps = 1e-6
i = 1
while torch.norm(nu_old-nu) > eps:
  nu_old = nu.clone()
  optimizer.zero_grad()
  f_of_nu = -(0.5*torch.norm(-torch.relu(-(x-nu)))**2 + nu*(torch.sum(x) -1) -0.5*x.size()[0]*nu**2)
  f_of_nu.backward()
  optimizer.step()
  print(f'At step {i+1:2} the function value is {f_of_nu.item(): 1.4f} and nu={nu: 0.4f}' )
  i += 1

y_star = torch.relu((x-nu)).cpu().detach()
print(y_star)
print(list(map(lambda x: round(x, 4), y_star.tolist())))
print(y_star.sum())

And the output gives:

...
At step 25 the function value is -2.0721 and nu= 0.2328
tensor(0.2328, requires_grad=True)
tensor([0.4285, 0.0341, 0.0000, 0.3885, 0.0000, 0.0000, 0.0000, 0.1489, 0.0000,
        0.0000])
[0.4285, 0.0341, 0.0, 0.3885, 0.0, 0.0, 0.0, 0.1489, 0.0, 0.0]
tensor(1.0000)