How to evaluate the trust-constr Lagrangian?

Question

I'm using the trust-constr algorithm from scipy.optimize.minimize with an interval constraint (lowerbound < g(x) < upperbound). I would like to plot the Lagrangian in a region around the found solution to analyze the convergence behavior.

According to my knowledge, the Lagrangian is defined as:

formula

with:

formula

In the returned OptimizeResult object, I can find the barrier parameter, but the slack variables are missing. The Lagrange multipliers are present, but there is only one per interval constraint, while I would expect two since each interval constraint is converted to two canonical inequality constraints:

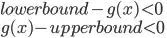
formula

Clearly, I'm missing something, so any help would be appreciated.

Minimal reproducible example:

import scipy.optimize as so
import numpy as np

# Problem definition:
# Five 2D points are given, with equally spaced x coordinates.
# The y coordinate of the first point is zero, while the last point has value 10.
# The goal is to find the smallest y coordinate of the other points, given the
# difference between the y coordinates of two consecutive points has to lie within the
# interval [-3, 3].

xs = np.linspace(0, 4, 5)
y0s = np.zeros(xs.shape)
y0s[-1] = 10

objective_fun = lambda y: np.mean(y**2)

def constraint_fun(ys):
    '''
    Calculates the signed squared consecutive differences of the input vector, augmented
    with the first and last element of y0s.
    '''
    full_ys = y0s.copy()
    full_ys[1:-1] = ys
    consecutive_differences = full_ys[1:] - full_ys[:-1]
    return np.sign(consecutive_differences) * consecutive_differences**2

constraint = so.NonlinearConstraint(fun=constraint_fun, lb=-3**2, ub=3**2)

result = so.minimize(method='trust-constr', fun=objective_fun, constraints=[constraint], x0=y0s[1:-1])

# The number of interval constraints is equal to the size of the output vector of the constraint function.
print(f'Nr. of interval constraints: {len(constraint_fun(y0s[1:-1]))}')

# Expected nr of Lagrange multipliers: 2x number of interval constraints.
print(f'Nr. of Lagrange multipliers: {len(result.v[0])}')

Output:

Nr. of interval constraints: 4
Nr. of Lagrange multipliers: 4

Expected output:

Nr. of interval constraints: 4
Nr. of Lagrange multipliers: 8

Can you please provide a minimal reproducible example where you think there are missing lagrangian multipliers? Note also that you can easily compute the slack variables s on your own because g(x) + s = 0. — joni, Mar 08 '22 at 12:51
@joni I've added the example. g(x) + s = 0 is the equality constraint originating from the inequality constraint g(x) < 0, but doesn't that mean that the algorithm will try to satisfy that equality constraint, not that it is necessarily exactly true (especially when not converged, but even at convergence)? — JulesTheGreat, Mar 08 '22 at 14:36

score 0 · Answer 1 · answered Mar 08 '22 at 15:52

You're right, there should indeed be 8 lagrangian multipliers. As a workaround, you can use the old dictionary constraints instead of the NonlinearConstraint objects.

lb, ub = -3**2, 3**2
# Note that lb <= g(x) <= ub is equivalent to g(x) - lb >= 0, ub - g(x) >= 0
cons = [{'type': 'ineq', 'fun': lambda ys: constraint_fun(ys) - lb},
        {'type': 'ineq', 'fun': lambda ys: ub - constraint_fun(ys)}]

res = minimize(objective_fun, method="trust-constr", x0=y0s[1:-1], constraints=cons)

Here, 'fun' is expected to be a function such that fun(x) >= 0. This gives me 8 lagrangian multipliers as expected. Nonetheless, it should also work with NonlinearConstraints, so it might be worth opening an issue at the scipy repo on Github.

Regarding your second question: res.constr contains a list of the constraint values at the solution, i.e. the values of g(x) - lb and ub - g(x). Since we have g(x) - lb - s = 0 and ub-g(x)-s=0 it follows immediately that res.constr are just the values of the slack variables you are looking for (when we use dictionary constraints).

How to evaluate the trust-constr Lagrangian?

1 Answers1