Using the smooth dice function as proposed in the V-Net paper:
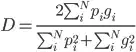
encoded for multiple classes in pytorch with a smooth added so that it is always divisable:
class DiceLoss(torch.nn.Module):
def __init__(self, smooth=1):
super(DiceLoss, self).__init__()
self.smooth = smooth
def forward(self, inputs, targets):
assert inputs.shape == targets.shape, f"Shapes don't match {inputs.shape} != {targets.shape}"
inputs = inputs[:,1:] # skip background class
targets = targets[:,1:] # skip background class
axes = tuple(range(2, len(inputs.shape))) # sum over elements per sample and per class
intersection = torch.sum(inputs * targets, axes)
addition = torch.sum(torch.square(inputs) + torch.square(targets), axes)
return 1 - torch.mean((2 * intersection + self.smooth) / (addition + self.smooth))
The target is volumetric sample patches of size 52^3 = 140.608. The samples are non overlapping from a volume with 97% background, 2% liver and 1% tumor. As a result most patches will be completely background. The dice loss is bound between 0 and 1.
Other questions set the smoothness to 1.0 or much lower 1e-7
Suppose a patch is fully background (as are most) and the prediction is 0.01 (=1%) liver and 0.01 tumor for all elements. Setting the smoothness to 1.0 will still result in
1 - (2 x 0 + 1) / (0 + 140.608 x 0.0001 + 1) = 0.9336
Close to the maximum loss even though the prediction is accurate.
This forces the network to decrease the likelihood of a liver or tumor to 0.001 or lower. What is the commonly used as a smoothness setting for the dice loss?