How to calculate R-square value for the exponential and power trendline types

Question

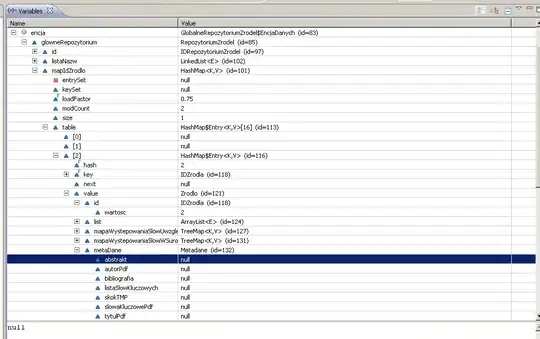
Tried to calculate the R-squared value for the exponential and power trendline type using the following equation.

   R² = ∑(ȳ - ŷ)² / ∑(y - ȳ)²

Here ȳ is the mean value of y and ŷ is the regression equation, here ŷ for exponential is y = ae^xb and for power is y = ax^b Here a = intercept and b = slope.

I have implemented the following code snippet logic to achieve the R squared value

  List<int> xValue = <int>[1,2,3,4,5];
List<int> yValue = <int>[2,4,5,4,5];
int sumOfX = 0,sumOfY = 0,sumOfXY = 0, sumOfXSquare = 0, sumOfYSquare = 0;
double slope = 0.5204, intercept = 2.3133;
for(int i = 0; i < xValue.length; i++){
    sumOfX += xValue[i];
    sumOfY += yValue[i];
    sumOfXY += xValue[i] * yValue[i];
    sumOfXSquare += math.pow(xValue[i], 2).toInt();
    sumOfYSquare += math.pow(yValue[i], 2).toInt();
 }
double yMean = sumOfY/yValue.length;
// value of ∑(y - ȳ)²
double ssTol = 0;
for(int j = 0; j < yValue.length; j++){
  ssTol += math.pow((yValue[j] - yMean),2);
 }
// value of ∑(ȳ - ŷ)²
double ssReg = 0;
for(int k = 0; k < yValue.length; k++){
  ssReg += math.pow(((intercept * math.pow(xValue[k], slope)) -yMean), 2).toDouble();
 }
print(ssReg/ssTol);
          

I want the R-squared value like below.

Can anyone please help me with this?

Answer 1

The correct equation for Rsq is Also, in the most current version of Excel, the Rsquared for your dataset is .7704 not .6782.

Additionally, Rsquared is only valid for linear regression Models. See Cross Validated Explanation

However, the power equation can be converted to linear. The Power regression model is in the form ...

y=ax^B

Take the log of both sides

ln(y) = ln(a) + b*ln(x)

This model can now be fit with linear regression. You might think that the ln(x) part would make linear regression inappropriate, however, linear regression means that it is linear in parameters. See this link for more information

With this form, it is now possible to fit the regression line with linear regression and use the equation for R Squared.

Start by taking the log of both x and y.

Fit a linear model to the new dataset. Note the Rsq is .7704 as it was above.

Recall that our power model is in the form y=ax^B

B = .5204 (coefficient for X in linear model)

Reason: we took the log of x^B which results in B*ln(X).

a = e^.8387 = 2.3133

Reason: we took the log of a which results in ln(a). The ln(a) = .8387. To get "a" we calculate e^ln(a) = a.

Finally, follow the equation above, to calculate Rsq. Here are some intermediate results to check against your code.

Answer 2

You could extract the R2 from the chart by the method suggested by Bas Verlaat

If you want to calculate youself, you may use either the following formula (but there is a difference with the one provided in the chart)

=CORREL(A2:A6,C2:C6)^2

=RSQ(A2:A6,C2:C6)