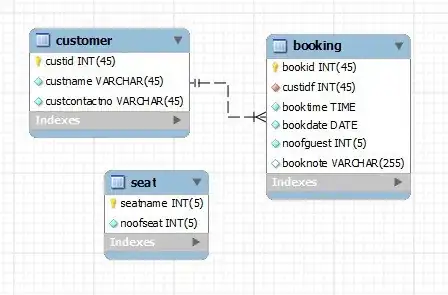
Here we have the Spatial domain implementation of Gabor filter. But, I need to implement a Gabor filter in the Frequency Domain for performance reasons.
I have found the Frequency Domain equation of Gabor Filter:
I am actually in doubt about the correctness and/or applicability of this formula.
Source Code
So, I have implemented the following :
public partial class GaborFfftForm : Form
{
private double Gabor(double u, double v, double f0, double theta, double a, double b)
{
double rad = Math.PI / 180 * theta;
double uDash = u * Math.Cos(rad) + v * Math.Sin(rad);
double vDash = (-1) * u * Math.Sin(rad) + v * Math.Cos(rad);
return Math.Exp((-1) * Math.PI * Math.PI * ((uDash - f0) / (a * a)) + (vDash / (b * b)));
}
public Array2d<Complex> GaborKernelFft(int sizeX, int sizeY, double f0, double theta, double a, double b)
{
int halfX = sizeX / 2;
int halfY = sizeY / 2;
Array2d<Complex> kernel = new Array2d<Complex>(sizeX, sizeY);
for (int u = -halfX; u < halfX; u++)
{
for (int v = -halfY; v < halfY; v++)
{
double g = Gabor(u, v, f0, theta, a, b);
kernel[u + halfX, v + halfY] = new Complex(g, 0);
}
}
return kernel;
}
public GaborFfftForm()
{
InitializeComponent();
Bitmap image = DataConverter2d.ReadGray(StandardImage.LenaGray);
Array2d<double> dImage = DataConverter2d.ToDouble(image);
int newWidth = Tools.ToNextPowerOfTwo(dImage.Width) * 2;
int newHeight = Tools.ToNextPowerOfTwo(dImage.Height) * 2;
double u0 = 0.2;
double v0 = 0.2;
double alpha = 10;//1.5;
double beta = alpha;
Array2d<Complex> kernel2d = GaborKernelFft(newWidth, newHeight, u0, v0, alpha, beta);
dImage.PadTo(newWidth, newHeight);
Array2d<Complex> cImage = DataConverter2d.ToComplex(dImage);
Array2d<Complex> fImage = FourierTransform.ForwardFft(cImage);
// FFT convolution .................................................
Array2d<Complex> fOutput = new Array2d<Complex>(newWidth, newHeight);
for (int x = 0; x < newWidth; x++)
{
for (int y = 0; y < newHeight; y++)
{
fOutput[x, y] = fImage[x, y] * kernel2d[x, y];
}
}
Array2d<Complex> cOutput = FourierTransform.InverseFft(fOutput);
Array2d<double> dOutput = Rescale2d.Rescale(DataConverter2d.ToDouble(cOutput));
//dOutput.CropBy((newWidth-image.Width)/2, (newHeight - image.Height)/2);
Bitmap output = DataConverter2d.ToBitmap(dOutput, image.PixelFormat);
Array2d<Complex> cKernel = FourierTransform.InverseFft(kernel2d);
cKernel = FourierTransform.RemoveFFTShift(cKernel);
Array2d<double> dKernel = DataConverter2d.ToDouble(cKernel);
Array2d<double> dRescaledKernel = Rescale2d.Rescale(dKernel);
Bitmap kernel = DataConverter2d.ToBitmap(dRescaledKernel, image.PixelFormat);
pictureBox1.Image = image;
pictureBox2.Image = kernel;
pictureBox3.Image = output;
}
}
Just concentrate on the algorithmic steps at this time.
I have generated a Gabor kernel in the frequency domain. Since, the kernel is already in Frequency domain, I didn't apply FFT to it, whereas image is FFT-ed. Then, I multiplied the kernel and the image to achieve FFT-Convolution. Then they are inverse-FFTed and converted back to Bitmap as usual.
Output
- The kernel looks okay. But, The filter-output doesn't look very promising (or, does it?).
- The orientation (theta) doesn't have any effect on the kernel.
- The calculation/formula is frequently suffering from divide-by-zero exception up on changing values.
How can I fix those problems?
Oh, and, also,
- what do the parameters α, β, represent?
- what should be the appropriate value of f0?
Update:
I have modified my code according to @Cris Luoengo's answer.
private double Gabor(double u, double v, double u0, double v0, double a, double b)
{
double p = (-2) * Math.PI * Math.PI;
double q = (u-u0)/(a*a);
double r = (v - v0) / (b * b);
return Math.Exp(p * (q + r));
}
public Array2d<Complex> GaborKernelFft(int sizeX, int sizeY, double u0, double v0, double a, double b)
{
double xx = sizeX;
double yy = sizeY;
double halfX = (xx - 1) / xx;
double halfY = (yy - 1) / yy;
Array2d<Complex> kernel = new Array2d<Complex>(sizeX, sizeY);
for (double u = 0; u <= halfX; u += 0.1)
{
for (double v = 0; v <= halfY; v += 0.1)
{
double g = Gabor(u, v, u0, v0, a, b);
int x = (int)(u * 10);
int y = (int)(v * 10);
kernel[x,y] = new Complex(g, 0);
}
}
return kernel;
}
where,
double u0 = 0.2;
double v0 = 0.2;
double alpha = 10;//1.5;
double beta = alpha;
I am not sure whether this is a good output.