0

I have a code in double-precision complex arithmetic that forms large, sparse matrices (thanks to PETSc) in order to solve problems where high accuracy is typically needed (results converged to 7/8 digits, say)

The resulting linear system Ax=b is solved by means of parallel LU decomposition. I'm aiming at solving large 3D problems so the leading dimension of the matrix can reach several dozens of millions.

The matrix contains elements resulting from the weights of the finite-difference method multiplied by the coefficients of the different physical equations solved and metric terms.

If one matrix entry is lower in absolute value than the double-precision machine accuracy, I discard it and chop it to zero. Would you consider that a sane approach, or, at the very least, pointless? One reason is that we want to save every possible MegaByte of memory. But what's open to debate is whether

  • 'Very small' entries might contaminate the LU inversion process and make it unstable while increasing fill-in.

  • If matrix entries close to machine precision are used in the process, I would assume that the result of any arithmetic operation involving those entries can be considered "unreliable"? If yes I don't see why they should be kept.

I'm aware that machine precision is a different concept than smallest representable positive number. Therefore it's possible my reasoning is conceptually wrong and would enjoy having your opinion or corrections. Thanks!

circuitbreaker
  • 183
  • 7
  • Not by me (don't know enought about it), but this might get voted down or closed because it seems to be a matter of opinion, and that is off-topic here. – Rudy Velthuis Jul 25 '18 at 17:32
  • The absolute “machine epsilon” is generally not a correct threshold to use. We do not know whether the significant values in your matrix tend to be around 1, 1e-20, or 1e20, so we do not know what they are relative to the machine epsilon. It is more appropriate to set a threshold that is **around** the magnitude of the significant values in your computations multiplied by the machine epsilon. What “around” means is context dependent. Any single operation has a maximum error of ½ an epsilon, but the compounding of several operations can produce larger errors… – Eric Postpischil Jul 25 '18 at 18:48
  • … If your LU inversion is numerically unstable, then any changes are bad. Any small values that have occurred due to rounding errors are nonetheless useful information that is the best the floating-point arithmetic could produce. In other words, they should not be considered unreliable. Low information is better than on information. Discarding them would discard information, which is likely to move the computed results away from the correct answers, and unstable processes compound errors. So the real question is can your computation tolerate small changes well, and will the resulting… – Eric Postpischil Jul 25 '18 at 18:53
  • … performance increase be worth the decreased quality of the result. That is something that requires more information to answer. – Eric Postpischil Jul 25 '18 at 18:53
  • @EricPostpischil: Consider making it an answer, even if the question is perhaps a but off topic. – President James K. Polk Jul 26 '18 at 12:44
  • @JamesKPolk: It’s a bit outside my usual practice areas, so I am not prepared to write authoritatively, at least not until the question is elaborated somewhat and others have a chance to answer. – Eric Postpischil Jul 26 '18 at 13:14

1 Answers1

0

The answer to this question is "it depends", as other people have already suggested. It is, however, possible to state precisely what the answer depends on.

Assume you want to solve the linear system,

Ax = b ,

where A and b are a matrix and a vector of proper dimensions. Now, you solve the perturbed linear system

(A + E)\hat x = b ,

where the perturbation matrix E fulfills that

\| E \|_\infty \le \alpha \| A \|_\infty .

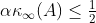If \alpha \kappa_\infty(A) \le \tfrac12, then

\frac{\| x - \hat x \|_\infty}{\| x \|_\infty} \le 4 \alpha\,\kappa_\infty(A) ,

where http://latex.codecogs.com/png.latex?%5Ckappa_%5Cinfty%28A%29 is the condition of A measured in the row-sum norm.

(This result can, e.g., be found in Golub, van Loan Matrix Computations Chapter 3.)

In other words, if you change the entries of the matrix, the result will change by the summed perturbations per row (\| \cdot \|_\infty is the row-sum norm), multiplied by a multiple of the condition of the matrix.

Hence, the perturbation of the matrix is allowed, if the summed perturbation per row relative to the row-sum norm of A is still small when multiplied by the condition of the matrix.

This result holds, of course, only for exact computations. However, as we have seen, in order to be allowed to perturbe the matrix, the condition number of the matrix should be sufficiently small. Thus, in this case if the perturbation is small, the condition number of the pertrubed matrix will also be small, and in this case the LU-decomposition poses no problems.

H. Rittich
  • 814
  • 7
  • 15