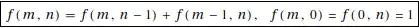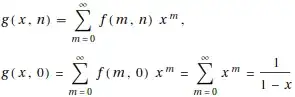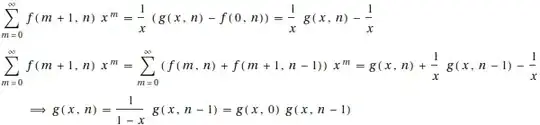3

I have a recurrence such as following:

RSolve[{f[m, n] == f[m, n - 1] + f[m - 1, n], 
        f[0, n] == 1, f[m, 0] == 1}, 
        f[m, n], {n}]

I tried to use RSolve, but I got an error:

RSolve::deqx: Supplied equations are not difference equations 
              of the given functions.

Appreciate your help!

Dr. belisarius
  • 60,527
  • 15
  • 115
  • 190
Qiang Li
  • 10,593
  • 21
  • 77
  • 148
  • I don't know mathematica, but the last two entries don't look like equations to me... – btilly Feb 09 '11 at 01:59
  • @btilly: what did you mean here? I am trying to give boundary conditions for the recurrence relation. – Qiang Li Feb 09 '11 at 02:32
  • @btilly the last two entries in the RSolve are the function to solve for and the free variables. As pointed out by @Alexey, the last one should be {m,n}. – Simon Feb 09 '11 at 05:42
  • Thanks, Simon. As I said, I don't know Mathematica. I was just looking at the error message and looking for something that /might/ fit. – btilly Feb 09 '11 at 06:01
  • 2
    Perhaps you may take a look at http://www.risc.jku.at/research/combinat/software/Guess/index.php – Dr. belisarius Feb 12 '11 at 14:15
  • @belisarius: I just came back to this question to suggest some of the packages at [RISC](http://www.risc.jku.at/research/combinat/risc/software/) - but you've beaten me to it! – Simon Mar 07 '11 at 23:38
  • @Simon Did you see http://www.imdb.com/title/tt1385826/ ?:D – Dr. belisarius Mar 08 '11 at 05:08
  • @belisarius: Saw a review of it... do you think some shadowy conspiracy is trying to get us to link to RISC? – Simon Mar 08 '11 at 05:10
  • @Simon Nahhhh ... I just mean I read your mind :) – Dr. belisarius Mar 08 '11 at 05:17

2 Answers2

9

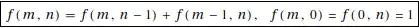
The difference equation and initial conditions are difference equation

Mathematica (7 and 8) does not like solving it... both with and without initial conditions. The RSolve expressions are left unevaluated

In[1]:= RSolve[{f[m,n]==f[m,n-1]+f[m-1,n],f[0,n]==f[m,0]==1},f[m,n],{m,n}]
        RSolve[{f[m,n]==f[m,n-1]+f[m-1,n]},f[m,n],{m,n}]
Out[1]= RSolve[{f[m,n]==f[-1+m,n]+f[m,-1+n],f[0,n]==f[m,0]==1},f[m,n],{m,n}]
Out[2]= RSolve[{f[m,n]==f[-1+m,n]+f[m,-1+n]},f[m,n],{m,n}]

I know that Mathematica uses generating functional methods (probably among other things) to solve such recurrences, but I don't know why it fails in such a simple case.

So let's do it by hand.

Let g(x,n) be the generating function for f(m,n)
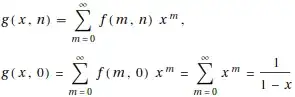
enter image description here

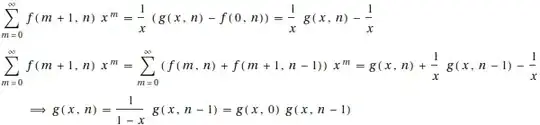
Now examine the sum of f(m+1,n) x^m enter image description here

Now solve the simple algebraic-difference equation: enter image description here

Which can also be done with RSolve

In[3]:= RSolve[g[x,n]-x g[x,n]==g[x,n-1]&&g[x,0]==1/(1-x),g[x,n],n];
        Simplify[%,Element[n,Integers]]
Out[4]= {{g[x,n]->(1-x)^(-1-n)}}

Now extract the coefficient of x^m:

In[5]:= SeriesCoefficient[(1 - x)^(-1 - n), {x, 0, m}]
Out[5]= Piecewise[{{(-1)^m*Binomial[-1 - n, m], m >= 0}}, 0]

The binomial is simplified using 

In[6]:= FullSimplify[(-1)^m*Binomial[-n - 1, m] == Binomial[m + n, m], Element[{n,m}, Integers]&&m>0&&n>0 ]
Out[6]= True

So we finally get Results!

This can be checked using symbolic and numeric means

In[7]:= ff[m_,n_]:=ff[m,n]=ff[m-1,n]+ff[m,n-1]
        ff[0,_]:=1;ff[_,0]:=1
In[9]:= And@@Flatten[Table[ff[m,n]==Binomial[n+m,m],{n,0,20},{m,0,20}]]
Out[9]= True

In[10]:= {f[m,n]==f[m,n-1]+f[m-1,n],f[0,n]==f[m,0]==1}/.f->(Binomial[#1+#2,#1]&)//FullSimplify
Out[10]= {True,True}
Simon
  • 14,631
  • 4
  • 41
  • 101
  • @Qiang Li: I know you probably know how to do it by hand... but I had made such a nice notebook... – Simon Feb 09 '11 at 06:59
  • @Simon, I appreciate your effort. But you, instead of mma, did most of the work. :) – Qiang Li Feb 09 '11 at 20:39
  • +1, I have to look at generating functions, I've never used them. – rcollyer Feb 09 '11 at 20:42
  • 1
    @Qiang Li: I've found that mma is useful for doing a lot of things, and can often lead you in directions you would never have thought of. However, I have found that spending a little extra time examining the problem by hand gives superior results. But, that's true of any programming language. – rcollyer Feb 09 '11 at 20:46
  • @rcollyer: I've never used them enough. The book I linked to, [generatingfunctionology](http://www.math.upenn.edu/~wilf/DownldGF.html) and [Wilf's](http://www.math.upenn.edu/~wilf/) other book [A=B](http://www.math.upenn.edu/~wilf/AeqB.html) (written with others) are definitely worth reading. – Simon Feb 09 '11 at 21:15
2

Not the answer but it seems that the right form should be (note {m, n} at the end):

RSolve[{f[m, n] == f[m, n - 1] + f[m - 1, n], f[0, n] == 1, f[m, 0] == 1}, f[m, n], {m, n}]

Mathematica leaves this unevaluated. I think it just cannot solve this.

Alexey Popkov
  • 9,355
  • 4
  • 42
  • 93
  • but this is a very simple function, f[m,n]=Binomial[n+m,m]. Mma cannot solve it? – Qiang Li Feb 09 '11 at 05:54
  • I think that most CASs struggle to solve 2-variable recurrence relations... Don't know why though, this one's not that hard. – Simon Feb 09 '11 at 06:01