Here's an illustration of the steps taken thus far:
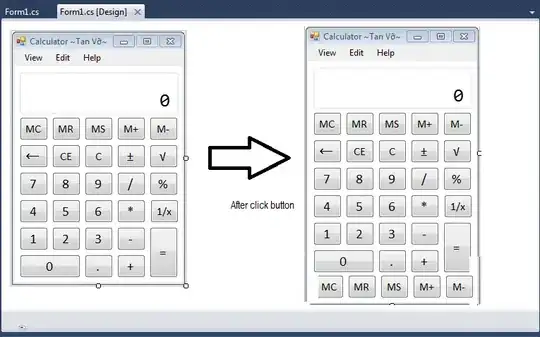
- Pseudo-random rectangle generation
- "Central node" insertion, rect separation, and final node selections
- Delaunay triangulation (shown with previously selected nodes)
- Rendering of triangle edges
At this point (Step 5), I would like to use this data to form a Minimum Spanning Tree, but there's a slight catch...
Somewhere in the graph (likely near the center, but not always) will be a node that requires between 3-5 connections to it from other unique nodes. This complicates things, since every other node should only contain a single connection, and the data structures being used make it difficult to determine "what's connected to what" in a solid, traversable format.
So, given an array of triangles in the above format, and a random vertex to use as the "root node", how could I properly traverse the network to create an MST where there are at least 3 connections to our "central node", but no more than 5 connections to it? Is this possible?