Take the "useful work done" at each recursion level to be some function f(n):

Let's observe what happens when we repeatedly substitute this back into itself.
T(n) terms:
 Spot the pattern?
Spot the pattern?
At recursion depth m:
- There are
 recursive calls to
recursive calls to T
- The first term in each parameter for
T is 
- The second term ranges from
 to
to 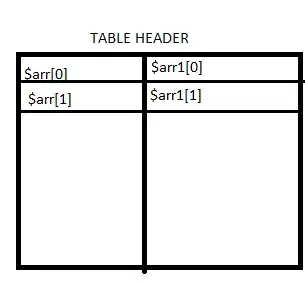 , in steps of
, in steps of 
Thus the sum of all T-terms at each level is given by:

f(n) terms:
Look familiar?
The f(n) terms are exactly one recursion level behind the T(n) terms. Therefore adapting the previous expression, we arrive at the following sum:
However note that we only start with one f-term, so this sum has an invalid edge case. However this is simple to rectify - the special-case result for m = 1 is simply f(n).
Combining the above, and summing the f terms for each recursion level, we arrive at the (almost) final expression for T(n):

We next need to find when the first summation for T-terms terminates. Let's assume that is when n ≤ c.
The last call to terminate intuitively has the largest argument, i.e the call to:

Therefore the final expression is given by:

Back to the original problem, what is f(n)?
You haven't stated what this is, so I can only assume that the amount of work done per call is ϴ(n) (proportional to the array length). Thus:
Your hypothesis was correct.
Note that even if we had something more general like
Where a is some constant not equal to 1, we would still have ϴ(n log n) as the result, since the  terms in the above equation cancel out:
terms in the above equation cancel out: