Find the order of a function

Question

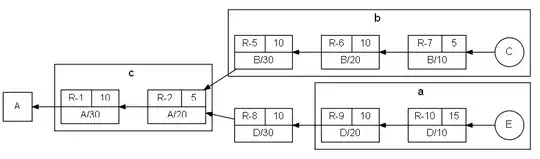
What is the lowest order of the following function as n tends to infinity?

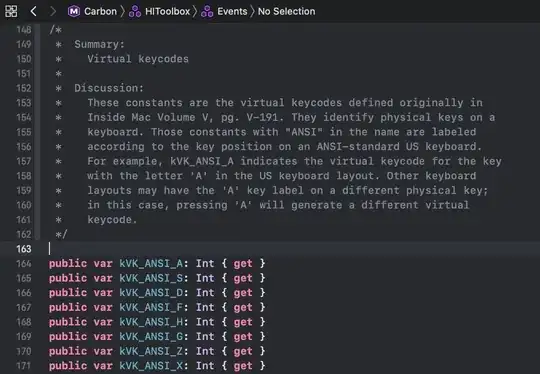
where a>1 and 0<p<1.

My answer: Since ln(1+x) <= x,

Therefore, f(n) = O(a^n). I am sure this is not a tight bound. I might be able to use to obtain a tighter bound, but I don't think it will improve the order. Any idea? Please let me know anything you think may be helpful.

If a<1, then f(n)<0. Maybe you mean a>1 rather than a>0? – sds Jul 17 '17 at 23:10 — sds, Jul 17 '17 at 23:10
@sds right. thanks for letting me know. – Sus20200 Jul 17 '17 at 23:15 — Sus20200, Jul 17 '17 at 23:15
Please move this question to [Math.SE] or [cstheory.SE]. – sds Jul 17 '17 at 23:21 — sds, Jul 17 '17 at 23:21

sds · Accepted Answer · 2017-07-19T14:39:54.557

2

Answer: O(n^2).

Proof:

f(n) = sum(i,log(pa^i+(1-p)))
     = sum(i,log(p*a^i(1+(1-p)/(pa^i))))
     =< sum(i,i*log(a)) + sum(i,log(p)) + sum(i,(1-p)/(pa^i))
     =< n*(n+1)*log(a)/2 + n*log(p) + (1-p)/p * 1/(1-1/a)

$\begin{align*} f(n) &= \sum_{i=0}^{i=n}\log(pa^i+(1-p)) \\ &= \sum_{i=0}^{i=n}\log(pa^i(1+\frac{1-p}{pa^i})) \\ &\le \sum_{i=0}^{i=n}i\log(a) + \sum_{i=0}^{i=n}\log(p) + \sum_{i=0}^{i=n}\frac{1-p}{pa^i} \\ &\le \frac{n(n+1)\log(a)}{2} + n\log(p) + \frac{1-p}{p} \times \frac{1}{1-\frac1a} \end{align*}$

This estimate is optimal because all inequalities are actually asymptotic equivalences.

Note that this is much smaller than your exponential estimate.

edited Jul 19 '17 at 14:39

answered Jul 17 '17 at 23:17

sds

58,617
29
161
278

That is great! How did you find it? – Sus20200 Jul 17 '17 at 23:24
@Sus20200: wdym? – sds Jul 17 '17 at 23:26
I meant I am surprised. – Sus20200 Jul 17 '17 at 23:45
Is that optimal? can we show no smaller order can be obtained? – Sus20200 Jul 17 '17 at 23:46
It's optimal because all inequalities are actually asymptotic equivalences. – sds Jul 17 '17 at 23:57
Thanks. BTW, you can use this http://www.codecogs.com/latex/eqneditor.php to produce images for each formula using latex and embed it here. – Sus20200 Jul 18 '17 at 13:15

Find the order of a function

1 Answers1