How to use plot_trisurf

Question

After updating matplotlib version from 1.3.1 to 2.0.2, when I want to use plot_trisurf to generate a TIN by 3d-points, I got an incomprehensible results. My test code is following:

import sys
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import numpy
from numpy.random import randn
from scipy import array, newaxis

chunk = numpy.loadtxt('test.xyz')  #test.xyz contains 38010 points,
DATA=numpy.array(chunk)
Xs = DATA[:,0]
Ys = DATA[:,1]
Zs = DATA[:,2]

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

surf = ax.plot_trisurf(Xs, Ys, Zs, cmap=cm.jet, linewidth=0)
fig.colorbar(surf)

ax.xaxis.set_major_locator(MaxNLocator(5))
ax.yaxis.set_major_locator(MaxNLocator(6))
ax.zaxis.set_major_locator(MaxNLocator(5))

fig.tight_layout()
plt.show()

The test.xyz file contains 38010 points. Some portion of it is showing as follows, the complete file can be found here.

512743.63 5403547.33 308.68
512743.62 5403547.33 308.70
512743.61 5403547.33 308.72
512743.60 5403547.34 308.68
512743.60 5403547.33 308.73
512741.50 5403547.36 309.05
512741.50 5403547.36 309.07
512741.49 5403547.46 309.09
512741.48 5403547.46 309.07
512741.47 5403547.46 309.10
512741.47 5403547.45 309.13
512741.46 5403547.37 309.04
512739.39 5403547.51 309.10
512739.39 5403547.48 309.34
512739.38 5403547.60 309.25
512739.37 5403547.71 309.15
512739.39 5403547.49 310.65
512739.39 5403547.48 310.70
512739.38 5403547.49 310.69
512739.37 5403547.48 310.72
512739.36 5403547.39 310.64
512739.32 5403547.41 309.20
512737.33 5403547.26 313.14
512737.33 5403547.37 313.09
512737.32 5403547.38 313.03
512737.30 5403547.37 313.12
512737.30 5403547.26 313.14
512735.22 5403547.41 311.72
512735.22 5403547.43 312.29
512735.22 5403547.49 312.59
512735.21 5403547.51 312.48
512735.20 5403547.60 312.53
512735.19 5403547.61 312.48
512735.18 5403547.72 312.40
512735.18 5403547.71 312.49
512735.17 5403547.71 312.51
512735.16 5403547.70 312.58
512735.15 5403547.61 312.52

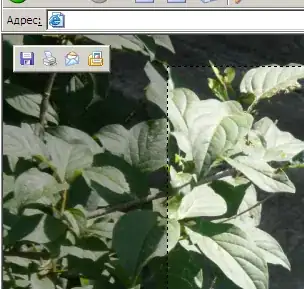
after updating, the result is shown as：

I think it is wrong, because I provide enough points to generate a TIN, but the result seems to use only a small part of the point. Before updating the matplotlib, I can get a result like:

Answer 1

Thanks a lot for all replies. This issue has been solved and the detailed was shown in Problem about plot_trisurf of matplotlib 2.0.2. And here I was pleasured to show my result. The problem is one of finite precision when calculating the Delaunay triangulation in qhull, which considers points that are near (according to a complicated definition of the word 'near') to be identical, so the triangulation is simpler than is desired. The dataset is an extreme one (in a bad way) for finite precision in that the spread of points about their mean is small (x.mean()=512767, x.max()-x.min()=134, y.mean()=303, y.max()-y.min()=5403707).This was explained by Ian Thomas. Thus, I have corrected my test code as follows:

import sys
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import numpy
from numpy.random import randn
from scipy import array, newaxis

chunk = numpy.loadtxt('test.xyz')  #test.xyz contains 38010 points,
DATA=numpy.array(chunk)
Xs = DATA[:,0]
Ys = DATA[:,1]
Zs = DATA[:,2]

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
#surf = ax.plot_trisurf(Xs, Ys, Zs, cmap=cm.jet, linewidth=0)
surf = ax.plot_trisurf(Xs-Xs.mean(), Ys-Ys.mean(), Zs, cmap=cm.jet, linewidth=0)
fig.colorbar(surf)

ax.xaxis.set_major_locator(MaxNLocator(5))
ax.yaxis.set_major_locator(MaxNLocator(6))
ax.zaxis.set_major_locator(MaxNLocator(5))

fig.tight_layout()
plt.show()

Before,the result was shown as:

After,the result was shown as:

So to sum this up, this was not actually an issue between different matplotlib versions and the current version is good enough to cope with the majority of use cases. And if someone hope that the axis ticklabes can be easily corrected for, you can refer to ImportanceOfBeingErnest's method.