The title of this post may be a bit confusing. Please allow me to provide a bit of context and then elaborate on what I'm asking. For your reference, the question I'm asking is toward the end and is denoted by bold letters. I provide some code, outlining where I'm currently at in solving the problem, immediately beforehand.
Essentially what I'm trying to do is Kernel Regression, which is usually done using a single test point x and a set of training instances 
. A reference to this can be found on wikipedia here. The kernel I'm using is the RBF kernel, a Wikipedia reference for which can be found here.
Anyway, I have some code written in Matlab so that this can be done quickly for a single instance of x, which is 1 x p in size. What I'd like to do is make it so I can estimate for numerous points very quickly, say m x p.
For the sake of avoiding notational mixups, I'll let the training instances be denoted Train and the instances I want estimates for as Test: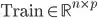 
and 
. It also needs to be mentioned that I want to estimate a vector of numbers for each of the m points. For a single point this vector would be 1 x v in size. Now I need it to be m x v. Therefore, Train will also have a vector of these know values associated with it called TS: 
. Lastly, we need a vector of sigmas that is 1 x v in size. This is denoted as Sig.
Here's the code I have so far:
%First, we have to get the matrices to equivalent size so we can subtract Train from Test
tm0 = kron(ones(size(Train,1),1),Test) - kron(ones(size(Test,1),1),Train);
%Secondly, we apply the Euclidean norm sq by row and then multiply each of these results by each element (j) in Sig times 1/2j^2
tm3 = exp(-kron(sum((tm0).^2,2),1/2./(Sig.^2)));
Now, at this point tm3 is an (m*n) x v matrix. This is where my question is: I now need to multiply TS' (TS transpose) times each of the n x v-sized segments in tm3 (there are m of these segments), get the diagonal elements of each of these resulting segments (after multiplication one of the m segments will be v x v, so each chunk of diagonal elements will be 1 x v meaning the resulting matrix is m x v) and sum these diagonal elements together to produce an m x 1 sized matrix. Lastly, I will need to divide each entry i in this m x 1 matrix by each of the v elements in the ith row of the diagonal-holding m x v-sized matrix, producing an m x v-sized result matrix.
I hope all of that makes sense. I'm sure there's some kind of trick that can be employed, but I'm just not coming up with it. Any help is greatly appreciated.
Edit 1: I was asked to provide more of an example to help demonstrate what it is that I would like done. The following represent that two matrices I'm talking about, TS and tm3:
As you can see, TS'(TS transpose) is v x n and tm3 is mn x v. In tm3 there are blocks that are of size n x v -- there are m blocks of this size. Notice that the size of TS' is of size v x n. This means that I can multiply TS' by a single block of tm3, which again is of size n x v. This would result in a matrix that is v x v in size. I would like to do this operation -- individually multiplying TS' by each of the n x v-sized blocks of tm3, which would produce m v x v matrices.
From here, though, I would like to obtain the diagonal elements from each of these v x v matrices. So, for a single v x v matrix, denoted using a:
Ultimately, I would to do this for each of the m v x v matrices giving me something that looks like the following, where s is the mth v x v matrix:
If I denote this last matrix as Q, which is m x v in size, it is trivial to sum the elements across the rows to produce the m x 1 vector I was looking for. I will refer to this vector as C. However, I would then like to divide each of these m scalar values by the corresponding row of matrix Q, to produce another m x v matrix:
This is the final matrix I'm looking for. Hopefully this helps make it clear what I'm looking for. Thanks for taking the time to read this!
Thought: I'm pretty sure I could accomplish this by converting tm3 to a cell matrix by doing tc1 = mat2cell(tm3,repmat(length(Train),1,m),length(Sig)), and then put replicate TS m times in another cell matrix tc2 = mat2cell(TS',length(indirectSigma),repmat(length(Train),1,m))'. Finally, I could do operations like tc3 = cellfun(@(a,b) a*b, tc2,tc1,'UniformOutput',false), which would give me m cells filled with the v x v matrices I was looking for. I could proceed from there. However, I'm not sure how fast these cell operations are. Can anybody comment? I'm afraid they might be slow, so I would prefer operations be performed on normal matrices, which I know to be fast. Thanks!
