I've gotten pretty far but something just doesn't seem to work.
A = 50.88259382849774,6.003988087177277
B = 50.88269282423443,6.0036662220954895
C = 50.882530369581545,6.003847271203995
The C coordinate is a little off from the 90 degree line (x) and this function I made should position C on the closest way to the x line.
this.snapCoords = function(a, b, c){
var result = (b.x-a.x)*(c.x-b.x)+(b.y-a.y)*(c.y-b.y);
var negative = false;
if(result < 0){
result = result*-1;
negative = true;
}
result = Math.sqrt(result);
result = result/2;
if(negative === false){
var d = {x: c.x+result, y: c.y-result};
}
else{
var d = {x: c.x-result, y: c.y+result};
}
console.log(d); // returns : 50.88246729610898,6.003910344676565
}
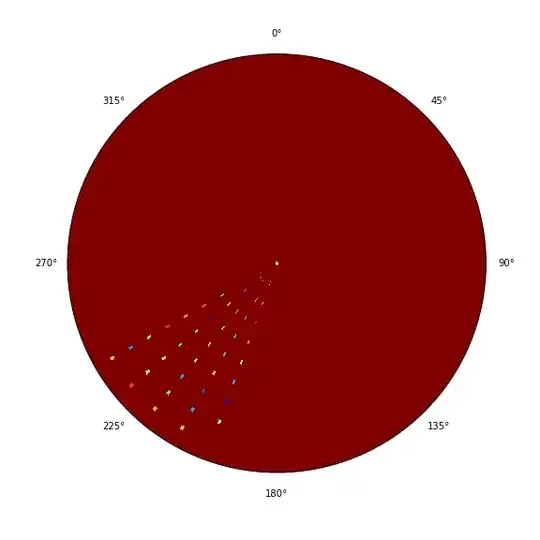
It does get the the 90 degree (x) line but not the closest way. Something must still be wrong in my function but I can't figure it out.
EDIT:
So this is my problem

My function puts the third coordinate on C which is 90 degrees but not where it should be (the red spot) it somehow extends to a further point.
