Calculating the Power spectral density

Question

I am trying to get the PSD of a real data set by making use of fftw3 library To test I wrote a small program as shown below ,that generates the a signal which follows sinusoidal function

#include <stdio.h>
#include <math.h>
#define PI 3.14

int main (){
    double  value= 0.0;
    float frequency = 5;
    int i = 0 ; 
    double time = 0.0;
    FILE* outputFile = NULL;
    outputFile = fopen("sinvalues","wb+");
    if(outputFile==NULL){
        printf(" couldn't open the file \n");
        return -1;
    }

    for (i = 0; i<=5000;i++){

        value =  sin(2*PI*frequency*zeit);
        fwrite(&value,sizeof(double),1,outputFile);
        zeit += (1.0/frequency);
    }
    fclose(outputFile);
    return 0;

}

Now I'm reading the output file of above program and trying to calculate its PSD like as shown below

#include <stdio.h>
#include <fftw3.h>
#include <complex.h>
#include <stdlib.h>
#include <math.h>
#define PI 3.14
int main (){
    FILE* inp = NULL;
    FILE* oup = NULL;
    double* value;// = 0.0;
    double* result;
    double spectr = 0.0 ;
    int windowsSize =512;
    double  power_spectrum = 0.0;
    fftw_plan plan;

    int index=0,i ,k;
    double multiplier =0.0;
    inp = fopen("1","rb");
    oup = fopen("psd","wb+");

    value=(double*)malloc(sizeof(double)*windowsSize);
    result = (double*)malloc(sizeof(double)*(windowsSize)); // what is the length that I have to choose here ? 
        plan =fftw_plan_r2r_1d(windowsSize,value,result,FFTW_R2HC,FFTW_ESTIMATE);

    while(!feof(inp)){

        index =fread(value,sizeof(double),windowsSize,inp);
            // zero padding 
        if( index != windowsSize){
            for(i=index;i<windowsSize;i++){
                    value[i] = 0.0;
                        }

        }


        // windowing  Hann 

        for (i=0; i<windowsSize; i++){
            multiplier = 0.5*(1-cos(2*PI*i/(windowsSize-1)));
            value[i] *= multiplier;
        }


        fftw_execute(plan);


        for(i = 0;i<(windowsSize/2 +1) ;i++){ //why only tell the half size of the window
            power_spectrum = result[i]*result[i] +result[windowsSize/2 +1 -i]*result[windowsSize/2 +1 -i];
            printf("%lf \t\t\t %d \n",power_spectrum,i);
            fprintf(oup," %lf \n ",power_spectrum);
        }

    }
    fclose(oup);
    fclose(inp);
    return 0;

}

Iam not sure about the correctness of the way I am doing this, but below are the results i have obtained:

Can any one help me in tracing the errors of the above approach

Thanks in advance *UPDATE after hartmut answer I'vve edited the code but still got the same result :

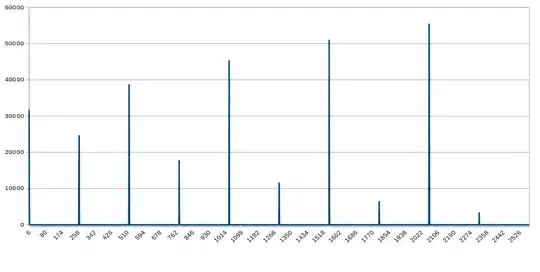
and the input data look like :

UPDATE after increasing the sample frequencyand a windows size of 2048 here is what I've got : UPDATE after using the ADD-ON here how the result looks like using the window :

Answer 1

You combine the wrong output values to power spectrum lines. There are windowsSize / 2 + 1 real values at the beginning of result and windowsSize / 2 - 1 imaginary values at the end in reverse order. This is because the imaginary components of the first (0Hz) and last (Nyquist frequency) spectral lines are 0.

int spectrum_lines = windowsSize / 2 + 1;
power_spectrum = (double *)malloc( sizeof(double) * spectrum_lines );

power_spectrum[0] = result[0] * result[0];
for ( i = 1 ; i < windowsSize / 2 ; i++ )
    power_spectrum[i] = result[i]*result[i] + result[windowsSize-i]*result[windowsSize-i];
power_spectrum[i] = result[i] * result[i];

And there is a minor mistake: You should apply the window function only to the input signal and not to the zero-padding part.

ADD-ON:

Your test program generates 5001 samples of a sinusoid signal and then you read and analyse the first 512 samples of this signal. The result of this is that you analyse only a fraction of a period. Due to the hard cut-off of the signal it contains a wide spectrum of energy with almost unpredictable energy levels, because you not even use PI but only 3.41 which is not precise enough to do any predictable calculation.

You need to guarantee that an integer number of periods is exactly fitting into your analysis window of 512 samples. Therefore, you should change this in your test signal creation program to have exactly numberOfPeriods periods in your test signal (e.g. numberOfPeriods=1 means that one period of the sinoid has a period of exactly 512 samples, 2 => 256, 3 => 512/3, 4 => 128, ...). This way, you are able to generate energy at a specific spectral line. Keep in mind that windowSize must have the same value in both programs because different sizes make this effort useless.

#define PI 3.141592653589793 // This has to be absolutely exact!

int windowSize = 512;        // Total number of created samples in the test signal
int numberOfPeriods = 64;    // Total number of sinoid periods in the test signal
for ( n = 0 ; n < windowSize ; ++n ) {
    value = sin( (2 * PI * numberOfPeriods * n) / windowSize );
    fwrite( &value, sizeof(double), 1, outputFile );
}

Answer 2

Some remarks to your expected output function.

• Your input is a function with pure real values. The result of a DFT has complex values. So you have to declare the variable out not as double but as fftw_complex *out.

• In general the number of dft input values is the same as the number of output values. However, the output spectrum of a dft contains the complex amplitudes for positive frequencies as well as for negative frequencies.

• In the special case for pure real input, the amplitudes of the positive frequencies are conjugated complex values of the amplitudes of the negative frequencies. For that, only the frequencies of the positive spectrum are calculated, which means that the number of the complex output values is the half of the number of real input values.

• If your input is a simple sinewave, the spectrum contains only a single frequency component. This is true for 10, 100, 1000 or even more input samples. All other values are zero. So it doesn't make any sense to work with a huge number of input values.

• If the input data set contains a single period, the complex output value is contained in out[1].

• If the If the input data set contains M complete periods, in your case 5, so the result is stored in out[5]

• I did some modifications on your code. To make some facts more clear.

---

#include <iostream>
#include <stdio.h>
#include <math.h>
#include <complex.h>
#include "fftw3.h"

int performDFT(int nbrOfInputSamples, char *fileName)
{
    int nbrOfOutputSamples;
    double *in;
    fftw_complex *out;
    fftw_plan p;

    // In the case of pure real input data,
    // the output values of the positive frequencies and the negative frequencies
    // are conjugated complex values.
    // This means, that there no need for calculating both.
    // If you have the complex values for the positive frequencies,
    // you can calculate the values of the negative frequencies just by
    // changing the sign of the value's imaginary part
    // So the number of complex output values ( amplitudes of frequency components)
    // are the half of the number of the real input values ( amplitutes in time domain):
    nbrOfOutputSamples = ceil(nbrOfInputSamples/2.0);

    // Create a plan for a 1D DFT with real input and complex output
    in = (double*) fftw_malloc(sizeof(double) * nbrOfInputSamples);
    out = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * nbrOfOutputSamples);
    p = fftw_plan_dft_r2c_1d(nbrOfInputSamples, in, out, FFTW_ESTIMATE);

    // Read data from input file to input array
    FILE* inputFile = NULL;
    inputFile = fopen(fileName,"r");
    if(inputFile==NULL){
        fprintf(stdout,"couldn't open the file %s\n", fileName);
        return -1;
    }
    double value;
    int     idx = 0;
    while(!feof(inputFile)){
        fscanf(inputFile, "%lf", &value);
        in[idx++] = value;       
    }
    fclose(inputFile);

    // Perform the dft
    fftw_execute(p);

    // Print output results
    char outputFileName[] = "dftvalues.txt";
    FILE* outputFile = NULL;
   outputFile = fopen(outputFileName,"w+");
    if(outputFile==NULL){
        fprintf(stdout,"couldn't open the file %s\n", outputFileName);
        return -1;
    }
    double  realVal;
    double  imagVal;
    double  powVal;
    double  absVal;

    fprintf(stdout, "     Frequency  Real       Imag        Abs       Power\n");
    for (idx=0; idx<nbrOfOutputSamples; idx++) {
        realVal = out[idx][0]/nbrOfInputSamples; // Ideed nbrOfInputSamples is correct!
        imagVal = out[idx][1]/nbrOfInputSamples; // Ideed nbrOfInputSamples is correct!
        powVal  = 2*(realVal*realVal + imagVal*imagVal);
        absVal  = sqrt(powVal/2);
        if (idx == 0) {
            powVal /=2;
        }
        fprintf(outputFile, "%10i %10.4lf %10.4lf %10.4lf %10.4lf\n", idx, realVal, imagVal, absVal, powVal);
        fprintf(stdout,     "%10i %10.4lf %10.4lf %10.4lf %10.4lf\n", idx, realVal, imagVal, absVal, powVal);
        // The total signal power of a frequency is the sum of the power of the posive and the negative frequency line.
        // Because only the positive spectrum is calculated, the power is multiplied by two.
        // However, there is only one single line in the prectrum for DC.
        // This means, the DC value must not be doubled.

    }
    fclose(outputFile);


    // Clean up
    fftw_destroy_plan(p);
    fftw_free(in); fftw_free(out);

    return 0;

}

int main(int argc, const char * argv[]) {
    // Set basic parameters
    float   timeIntervall = 1.0;     // in seconds
    int     nbrOfSamples = 50;      //  number of Samples per time intervall, so the unit is S/s
    double  timeStep = timeIntervall/nbrOfSamples; // in seconds
    float   frequency = 5;          // frequency in Hz

    // The period time of the signal is 1/5Hz = 0.2s
    // The number of samples per period is: nbrOfSamples/frequency = (50S/s)/5Hz = 10S
    // The number of periods per time intervall is: frequency*timeIntervall = 5Hz*1.0s = (5/s)*1.0s = 5



    // Open file for writing signal values
    char fileName[] = "sinvalues.txt";
    FILE* outputFile = NULL;
    outputFile = fopen(fileName,"w+");
    if(outputFile==NULL){
        fprintf(stdout,"couldn't open the file %s\n", fileName);
        return -1;
    }

    // Calculate signal values and write them to file
    double  time;
    double  value;
    double  dcValue = 0.2;
    int idx = 0;
    fprintf(stdout, "     SampleNbr   Signal value\n");
    for (time = 0; time<=timeIntervall; time += timeStep){
        value =  sin(2*M_PI*frequency*time) + dcValue;
        fprintf(outputFile, "%lf\n",value);
        fprintf(stdout, "%10i %15.5f\n",idx++, value);
    }
    fclose(outputFile);

    performDFT(nbrOfSamples, fileName);
    return 0;

}

• If the input of a dft is pure real, the output is complex in any case. So you have to use the plan r2c (RealToComplex).
• If the signal is sin(2*pi*f*t), starting at t=0, the spectrum contains a single frequency line at f, which is pure imaginary.
• If the sign has an offset in phase, like sin(2*pi*f*t+phi) the single line's value is complex.
• If your sampling frequency is fs, the range of the output spectrum is -fs/2 ... +fs/2.
• The real parts of the positive and negative frequencies are the same.
• The imaginary parts of the positive and negative frequencies have opposite signs. This is called conjugated complex.
• If you have the complex values of the positive spectrum you can calculate the values of the negative spectrum by changing the sign of the imaginary parts. For this reason there is no need to compute both, the positive and the negative sprectrum.
• One sideband holds all information. Therefore the number of output samples in the plan r2c is the half+1 of the number of input samples.

• To get the power of a frequency, you have to consider the positive frequency as well as the negative frequency. However, the plan r2c delivers only the right positive half of the spectrum. So you have to double the power of the positive side to get the total power.

  By the way, the documentation of the fftw3 package describes the usage of plans quite well. You should invest the time to go over the manual.

Answer 3

I'm not sure what your question is. Your results seem reasonable, with the information provided.

As you must know, the PSD is the Fourier transform of the autocorrelation function. With sine wave inputs, your AC function will be periodic, therefore the PSD will have tones, like you've plotted.

My 'answer' is really some thought starters on debugging. It would be easier for all involved if we could post equations. You probably know that there's a signal processing section on SE these days.

First, you should give us a plot of your AC function. The inverse FT of the PSD you've shown will be a linear combination of periodic tones.

Second, try removing the window, just make it a box or skip the step if you can.

Third, try replacing the DFT with the FFT (I only skimmed the fftw3 library docs, maybe this is an option).

Lastly, trying inputting white noise. You can use a Bernoulli dist, or just a Gaussian dist. The AC will be a delta function, although the sample AC will not. This should give you a (sample) white PSD distribution.

I hope these suggestions help.