I am trying to parallelize my image smoothing program recently
The algorithm to do this is easy to understand.
#define MAX_SMOOTH_LEVEL 1000
For i=0 to MAX_SMOOTH_LEVEL
For each pixel in rgb
Color rgb[IMG_HEIGHT][IMG_WIDTH], newrgb[IMG_HEIGHT][IMG_WIDTH];
new_rgb[i][j]=(rgb[i][j]+rgb[i-1][j]+rgb[i+1][j]+rgb[i][j+1]+rgb[j-1])/5;
Next
Next
if rgb[i-1][j] is out of bound(i-1<0), then use the color of rgb[imgHeight-1][j].. and so on....
The following picture is my idea to parallelize the computation. I think it is clear enough!
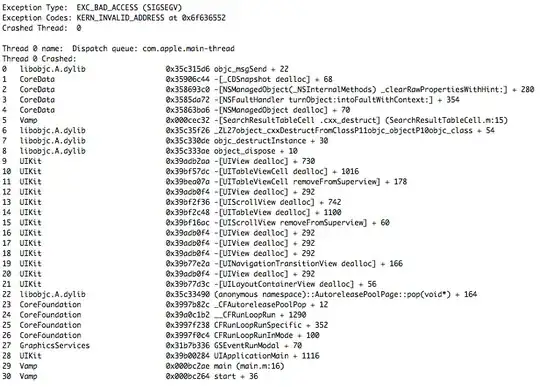
I would like to ask if my idea is reasonable? Do we really need to wait for all task to finish their work before next computation?
sorry for my bad English. I've tried hard to fix grammar errors