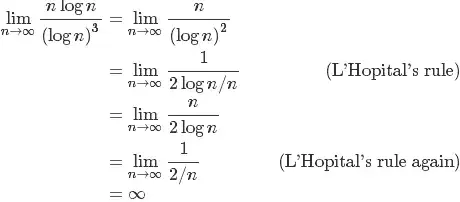Algorithm complexity, log^k n vs n log n

Question

I am developing some algorithm with takes up O(log^3 n). (NOTE: Take O as Big Theta, though Big O would be fine too)

I am unsure whereas O(log^3 n), or even O(log^2 n), is considered to be more/less/equaly complex as O(n log n).

If I were to follow the rules stright away, I'd say O(n log n) is the more complex one, but still, I don't have any clue as why or how.

I've done some research but I haven't been able to find an answer to this question.

Thank you very much.

nlogn is more complex neither log^2n, for example if we have N equals to 1024, we have 1024*10 > 10*10 (log base is 2) — Iłya Bursov, Nov 14 '13 at 19:21
@JohnKugelman Absolutely right. Please post that as an answer. Would O(n log n) be accepted as a Greedy algorithm? — , Nov 14 '13 at 19:25

score 12 · Accepted Answer · edited Nov 14 '13 at 20:11

12

Thus (n log n) is "bigger" than ((log n)³). This could be easily generalized to ((log n)^k) via induction.

edited Nov 14 '13 at 20:11

John Kugelman

349,597
67
533
578

answered Nov 14 '13 at 19:36

kennytm

510,854
105
1,084
1,005

John Kugelman · Answer 2 · 2013-11-14T19:37:00.287

9

If you graph the two functions together you can see that n log(n) grows faster than log³ n.

To prove this, you need to prove that n log n > log³ n for all values of n greater than some arbitrary number c. Find such a c and you have your proof.

In fact, n log(n) grows faster than any log^x n for positive x.

edited Nov 14 '13 at 19:37

answered Nov 14 '13 at 19:31

John Kugelman

349,597
67
533
578

Algorithm complexity, log^k n vs n log n

2 Answers2