I've been trying to fit a function to some data for a while using scipy.optimize.curve_fit but I have real difficulty. I really can't see any reason why this wouldn't work.
# encoding: utf-8
from __future__ import (print_function,
division,
unicode_literals,
absolute_import,
with_statement)
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as mpl
x, y, e_y = np.loadtxt('data.txt', unpack=True)
def f(x, a, k):
return (1/(np.sqrt(1 + a*((k-x)**2))))
popt, pcov = curve_fit(f, x, y, maxfev = 100000000)
mpl.plot(x, f(x, *popt), 'r-', label='Fit')
mpl.plot(x, y, 'rx', label='Original')
mpl.legend(loc='best')
mpl.savefig('curve.pdf')
print(popt)
# correct values which should be calculated
# a=0.003097
# k=35.4
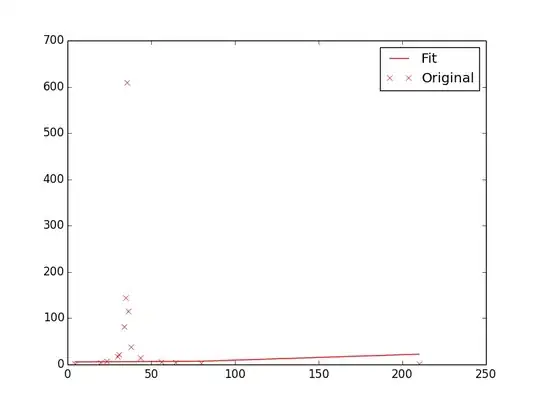
Here is the plot-image which is produced by upper code:
data.txt:
#x y e_y
4.4 0.79 0.13
19.7 4.9 0.8
23.5 7.3 1.2
29.7 17 2.79
30.7 21.5 3.52
34 81 13.28
34.6 145 23.77
35.4 610 100
36.3 115 18.85
38.1 38 6.23
43.7 14 2.3
56.2 6.2 1.02
64.7 4.6 0.75
79.9 3.2 0.52
210 0.98 0.16